题目内容
【题目】如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( ) 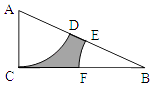
A.![]()
B.1﹣ ![]()
C.![]()
D.1﹣ ![]()
【答案】D
【解析】解:设AC=1,在Rt△ACB中,∠ACB=90°,BC=2AC=2, ∴S△ABC= ![]() ACBC=1,
ACBC=1,
∵分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,
∴扇形ACD+扇形BEF的面积等于以1为半径的圆的面积的四分之一,
∴S扇形ACD+S扇形BEF= ![]() ,
,
∴S阴影部分=1﹣ ![]() ,
,
∴在△ACB中任取一点,这一点恰好在图中阴影部分的概率是 ![]() =1﹣
=1﹣ ![]() ,
,
故选:D
【考点精析】利用几何概型对题目进行判断即可得到答案,需要熟知几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.

【题目】和谐高级中学共有学生570名,各班级人数如表:
一班 | 二班 | 三班 | 四班 | |
高一 | 52 | 51 | y | 48 |
高二 | 48 | x | 49 | 47 |
高三 | 44 | 47 | 46 | 43 |
已知在全校学生中随机抽取1名,抽到高二年级学生的概率是 ![]() .
.
(1)求x,y的值;
(2)现用分层抽样的方法在全校抽取114名学生,应分别在各年级抽取多少名?
【题目】某城市随机抽取一个月(30天)的空气质量指数API监测数据,统计结果如下:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | (300,350] |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 2 | 4 | 5 | 9 | 4 | 3 | 3 |
(Ⅰ)根据以上数据估计该城市这30天空气质量指数API的平均值;
(Ⅱ)若该城市某企业因空气污染每天造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系式为:
S= 
若在本月30天中随机抽取一天,试估计该天经济损失S大于200元且不超过600元的概率.


