题目内容
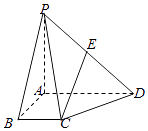
【题目】如图所示,在四棱锥P﹣ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点. 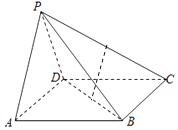
(1)证明:EF∥平面PAD;
(2)证明:直线PA⊥平面PCD.
【答案】
(1)证明:连结AC,则F也是AC的中点,
又E是PC的中点,∴EF∥PA,
又EF平面PAD,PA平面PAD,
∴EF∥平面PAD
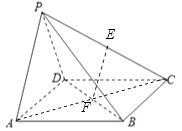
(2)证明:∵平面PAD⊥平面ABCD,CD⊥AD,面PAD∩面ABCD=AD,∴CD⊥面PAD,
∵PA面PAD,∴CD⊥PA,
∵∠APD=90°,
∴PA⊥PD,
∵CD∩PD=D,
∴PA⊥平面PCD
【解析】(1)根据线面平行的判定定理进行证明即可.(2)证明CD⊥PA,PA⊥PD,运用线面垂直的定理可证明.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.

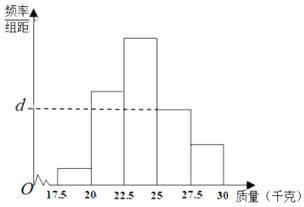
【题目】为了检测某种产品的质量(单位:千克),抽取了一个容量为N的样本,整理得到的数据作出了频率分布表和频率分布直方图如图:
分组 | 频数 | 频率 |
[17.5,20) | 10 | 0.05 |
[20,225) | 50 | 0.25 |
[22.5,25) | a | b |
[25,27.5) | 40 | c |
[27.5,30] | 20 | 0.10 |
合计 | N | 1 |
(Ⅰ)求出表中N及a,b,c的值;
(Ⅱ)求频率分布直方图中d的值;
(Ⅲ)从该产品中随机抽取一件,试估计这件产品的质量少于25千克的概率.