题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,都有
时,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)试问过点![]() 可作多少条直线与曲线
可作多少条直线与曲线![]() 相切?并说明理由.
相切?并说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)见解析,理由见解析
;(Ⅲ)见解析,理由见解析
【解析】
(Ⅰ)首先求出函数的定义域和导函数,根据导函数分类讨论![]() 的取值范围;当
的取值范围;当![]() 时,当
时,当![]() 时,分析
时,分析![]() 的正负即可求解.
的正负即可求解.
(Ⅱ)由(Ⅰ)中的导函数讨论![]() 是否在区间
是否在区间![]() 内,利用函数的单调性求出函数的最值,使
内,利用函数的单调性求出函数的最值,使![]() 即可解不等式即可.
即可解不等式即可.
(Ⅲ)法一:设切点为![]() ,求出切线方程
,求出切线方程 ,从而可得
,从而可得 ,令
,令![]() ,讨论
,讨论![]() 的取值范围,分析函数
的取值范围,分析函数![]() 的的单调性以及
的的单调性以及![]() 在
在![]() 上的零点即可求解;
上的零点即可求解;
法二:设切点为![]() ,求出切线方程
,求出切线方程 ,从而可得
,从而可得 ,分离参数可得
,分离参数可得![]() ,令
,令![]() ,讨论
,讨论![]() 的单调性求出函数
的单调性求出函数![]() 的值域,根据值域确定
的值域,根据值域确定![]() 的范围即可求解.
的范围即可求解.
(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
(1)当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 在
在![]() 上单调递增;
上单调递增;
(2)当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,函数
,函数![]() 为增函数.
为增函数.
综上所述,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(Ⅱ)由(Ⅰ)可知,
(1)当![]() 时,即
时,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
所以在区间![]() 上,
上,![]() ,显然函数
,显然函数![]() 在区间
在区间![]() 上恒大于零;
上恒大于零;
(2)当![]() 时,即
时,即![]() 时,函数
时,函数![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
所以![]() .
.
依题意有![]() ,解得
,解得![]() ,所以
,所以![]() .
.
(3)当![]() 时,即
时,即![]() 时,
时,![]() 在区间
在区间![]() 上为减函数,
上为减函数,
所以![]() .
.
依题意有![]() ,解得
,解得![]() ,所以
,所以![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上恒大于零.
上恒大于零.
另解:当![]() 时,显然
时,显然![]() 恒成立.
恒成立.
当![]() 时,
时,![]() 恒成立
恒成立![]() 恒成立
恒成立![]() 的最大值.
的最大值.
令![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 最大值为
最大值为![]() ,此时应有
,此时应有![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)设切点为![]() ,则切线斜率
,则切线斜率![]() ,
,
切线方程为 .
.
因为切线过点![]() ,则
,则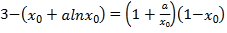 .
.
即 .①
.①
令![]() ,则
,则![]() .
.
(1)当![]() 时,在区间
时,在区间![]() 上,
上,![]() ,
,![]() 单调递增;
单调递增;
在区间![]() 上,
上,![]() ,
,![]() 单调递减,
单调递减,
所以函数![]() 的最大值为
的最大值为![]() .
.
故方程![]() 无解,即不存在
无解,即不存在![]() 满足①式.
满足①式.
因此当![]() 时,切线的条数为0.
时,切线的条数为0.
(2)当![]() 时,在区间
时,在区间![]() 上,
上,![]() ,
,![]() 单调递减,在区间
单调递减,在区间![]() 上,
上,![]() ,
,![]() 单调递增,
单调递增,
所以函数![]() 的最小值为
的最小值为![]() .
.
取![]() ,则
,则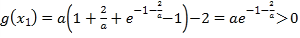 .
.
故![]() 在
在![]() 上存在唯一零点.
上存在唯一零点.
取![]() ,则
,则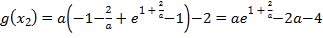
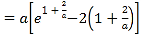 .
.
设![]() ,
,![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 恒成立.
恒成立.
所以![]() 在
在![]() 单调递增,
单调递增,![]() 恒成立.
恒成立.
所以![]() .
.
故![]() 在
在![]() 上存在唯一零点.
上存在唯一零点.
因此当![]() 时,过点
时,过点![]() 存在两条切线.
存在两条切线.
(3)当![]() 时,
时,![]() ,显然不存在过点
,显然不存在过点![]() 的切线.
的切线.
综上所述,当![]() 时,过点
时,过点![]() 存在两条切线;
存在两条切线;
当![]() 时,不存在过点
时,不存在过点![]() 的切线.
的切线.
另解:设切点为![]() ,则切线斜率
,则切线斜率![]() ,
,
切线方程为 .
.
因为切线过点![]() ,则
,则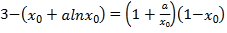 ,
,
即 .
.
当![]() 时,
时,![]() 无解.
无解.
当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() ,
,
易知当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又![]() ,且
,且![]() ,
,
故当![]() 时有两条切线,当
时有两条切线,当![]() 时无切线,
时无切线,
即当![]() 时有两条切线,当
时有两条切线,当![]() 时无切线.
时无切线.
综上所述,![]() 时有两条切线,
时有两条切线,![]() 时无切线.
时无切线.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科,某省采用![]() 模式,其中语文、数学、外语三科为必考科目,每门科目满分均为
模式,其中语文、数学、外语三科为必考科目,每门科目满分均为![]() 分.另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分.另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每门科目满分均为
),每门科目满分均为![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取
人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查,其中,女生抽取
名学生进行调查,其中,女生抽取![]() 人.
人.
(1)求![]() 的值;
的值;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的![]() 名学生进行问卷调查(假定每名学生在“物理”和“地理”这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的一个不完整的
名学生进行问卷调查(假定每名学生在“物理”和“地理”这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的一个不完整的![]() 列联表,请将下面的
列联表,请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“地理” | 总计 | |
男生 |
| ||
女生 |
| ||
总计 |
(3)在抽取到的![]() 名女生中,按(2)中的选课情况进行分层抽样,从中抽出
名女生中,按(2)中的选课情况进行分层抽样,从中抽出![]() 名女生,再从这
名女生,再从这![]() 名女生中抽取
名女生中抽取![]() 人,设这
人,设这![]() 人中选择“物理”的人数为
人中选择“物理”的人数为![]() ,求
,求![]() 的分布列及期望.附:
的分布列及期望.附:![]() ,
,![]()
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【题目】自湖北武汉爆发新型冠状病毒肺炎疫情以来,各地医疗物资缺乏,各生产企业纷纷加班加点生产,某企业准备购买三台口罩生产设备,型号分别为A,B,C,已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元;也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应同时购买的易耗品的件数,该单位调查了这三种型号的设备各60台,调查每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
频数 | 型号A | 30 | 30 | 0 |
型号B | 20 | 30 | 10 | |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中A,B,C三台设备使用的易耗品总数超过21件(不包括21件)的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?