题目内容
9.若0<x<y,且x+y=1,将x2+y2,2xy,x,y,$\frac{1}{2}$从小到大进行排列.分析 根据基本不等式的性质判断即可.
解答 解:若0<x<y,且x+y=1,
则x2+y2>2xy,
xy<${(\frac{x+y}{2})}^{2}$=$\frac{1}{4}$,
∴0<2xy<$\frac{1}{2}$
而0<x<$\frac{1}{2}$,$\frac{1}{2}$<y<1,
1<2y<2,
∴x•2y>x,
由x2+y2-y
=(1-y)2+y2-y
=2y2-3y+1
=2${(y-\frac{1}{3})}^{2}$+$\frac{7}{9}$>0,
∴x2+y2>y,
∴x<2xy<$\frac{1}{2}$<y<x2+y2.
点评 本题考查了基本不等式的性质的应用,是一道基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
19.已知函数f(x)=ax(a>0,a≠1)在区间[-2,2]上的函数值总小于2,则log2a的取值范围是( )
| A. | (-$\frac{1}{2}$,0)∪($\frac{1}{2}$,1) | B. | (0,$\frac{1}{2}$)∪($\frac{\sqrt{2}}{2}$,1) | C. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
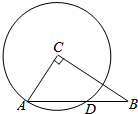 如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.
如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.