题目内容
【题目】已知函数![]()
(1)求![]() 的极值;
的极值;
(2)请填好下表(在答卷),并画出![]() 的图象(不必写出作图步骤);
的图象(不必写出作图步骤);

(3)设函数![]() 的图象与
的图象与![]() 轴有两个交点,求
轴有两个交点,求![]() 的值。
的值。
【答案】(1)见解析(2)当![]() 时
时![]() 有极大值7, 当
有极大值7, 当![]() 时
时![]() 有极小值-20(3)
有极小值-20(3)![]()
【解析】试题分析:(1)求导数![]() ,解方程
,解方程![]() 求出函数定义域内的所有根;列表检查
求出函数定义域内的所有根;列表检查![]() 在
在![]() 的根
的根![]() 左右两侧值的符号,如果左正右负(左增右减),那么
左右两侧值的符号,如果左正右负(左增右减),那么![]() 在
在![]() 处取极大值,如果左负右正(左减右增),那么
处取极大值,如果左负右正(左减右增),那么![]() 在
在![]() 处取极小值;(2)直接将表格中数据代入解析式,然后描点、连线即可;(3)由(1)知当
处取极小值;(2)直接将表格中数据代入解析式,然后描点、连线即可;(3)由(1)知当![]() 时
时![]() 有极大值
有极大值![]() , 当
, 当![]() 时
时![]() 有极小值
有极小值![]() ,可得函数
,可得函数![]() 的图象与
的图象与![]() 轴有两个交点时,
轴有两个交点时, ![]() 或
或![]() .
.
试题解析:(1)![]() ,令
,令![]() 得
得![]() -(2分)
-(2分)
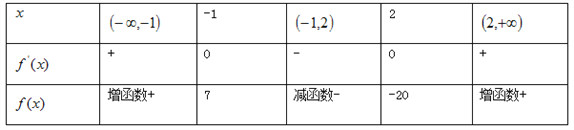
由表知,当![]() 时
时![]() 有极大值7, 当
有极大值7, 当![]() 时
时![]() 有极小值-20.
有极小值-20.
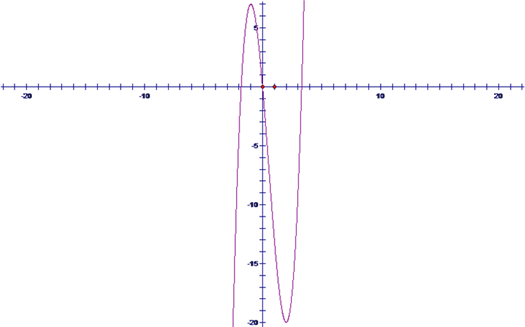
(2)

画对图
(3)由(1)知当![]() 时
时![]() 有极大值
有极大值![]() , 当
, 当![]() 时
时![]() 有极小值
有极小值![]() ,
,
再由(2)知,当![]() 的极大值或极小值为0时,函数
的极大值或极小值为0时,函数![]() 的图象与
的图象与![]() 轴有两个交点,即
轴有两个交点,即![]() .
.

练习册系列答案
相关题目
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请在图中画出上表数据的散点图;

![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
![]() 试根据
试根据![]() 求出的线性回归方程,预测记忆力为9的同学的判断力.
求出的线性回归方程,预测记忆力为9的同学的判断力.
相关公式: .
.
