Question

【题目】函数，且在处的切线斜率为.

(1)求的值，并讨论在上的单调性；

(2)设函数 ，其中，若对任意的总存在，使得成立，求的取值范围

（3）已知函数，试判断在内零点的个数.

Answer 1

【答案】(1)答案见解析；(2)答案见解析.（3）1个零点

【解析】试题分析：

(1)由函数的解析式可得f′(x)＝(a－1)sin x＋axcos x，由可得，利用导函数讨论单调性可得f(x)在， 上单调递增；在， 上单调递减．

(2)结合(1)的结论可知f(x)min＝f(0)＝1，则g(x)≥1在x∈[0，＋∞)上恒成立．且g′(x)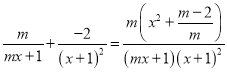＝ (x≥0，m>0)，据此讨论可知m≥2时满足题意，当0<m<2时不合题意，则的取值范围是m≥2.

(3)由函数的解析式可得： ，构造函数，则，据此讨论可得存在，当时， 单调递增，当时， 单调递减，结合端点函数在可得在内零点的个数为1个.

试题解析：

(1)∵f′(x)＝asin x＋axcos x－sin x＝(a－1)sin x＋axcos x，

f　′＝(a－1)·＋·a·＝，

∴a＝1，f′(x)＝xcos x.

当f′(x)>0时，－π<x<－或0<x<；

当f′(x)<0时，－<x<0或<x<π，

∴f(x)在，上单调递增；在，上单调递减．

(2)当x∈[0，]时，f(x)单调递增，∴f(x)min＝f(0)＝1，

则只需g(x)≥1在x∈[0，＋∞)上恒成立即可．

g′(x)＝ (x≥0，m>0)，

①当m≥2时，≥0，∴g′(x)≥0在[0，＋∞)上恒成立，即g(x)在[0，＋∞)上单调递增，又g(0)＝1，∴g(x)≥1在x∈[0，＋∞)上恒成立，故m≥2时成立．

②当0<m<2时，当x∈时，g′(x)<0，此时g(x)单调递减，∴g(x)<g(0)＝1，故0<m<2时不成立．

综上m≥2.

(3)由函数的解析式可得： ，

令，则，故函数单调递增，

当从右侧趋近于时， ， ，

故存在，满足，

当时， 单调递增，

当时， 单调递减，

且： ， ，

函数图象如图所示：

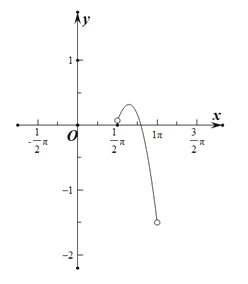
据此可得： 在内零点的个数为1个.