题目内容
已知函数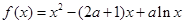 .
.
(1)求函数 在区间
在区间 上的最小值;
上的最小值;
(2)设 ,其中
,其中 ,判断方程
,判断方程 在区间
在区间 上的解的个数(其中
上的解的个数(其中 为无理数,约等于
为无理数,约等于 且有
且有 ).
).
(1) 时,
时,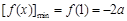 ,
, 时,
时,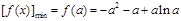 ,
, 时,
时, ;(2)方程
;(2)方程 在区间
在区间 上存在唯一解.
上存在唯一解.
解析试题分析:(1)先求出 并进行因式分解得到
并进行因式分解得到 ,然后分
,然后分 、
、 、
、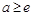 三类进行讨论函数在
三类进行讨论函数在 的单调性,从而确定函数的最小值;(2)设
的单调性,从而确定函数的最小值;(2)设 ,进而通过求导
,进而通过求导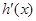 ,由
,由 确定函数
确定函数 在
在 的单调性,进而判断两端点函数值是正数还是负数,最终确定函数
的单调性,进而判断两端点函数值是正数还是负数,最终确定函数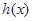 零点的个数即方程
零点的个数即方程 在
在 上的解的个数.
上的解的个数.
试题解析:(1)由

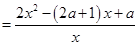
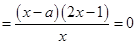 ,得
,得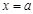 或
或
①当 时,
时,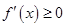 ,所以故
,所以故 在
在 上是增函数,所以
上是增函数,所以
②当 时,
时,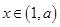 时,
时,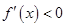 ;
;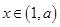 时,
时,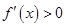
所以, 在
在 上是减函数,在
上是减函数,在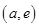 上是增函数,故
上是增函数,故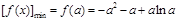
③当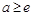 时,
时,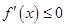 ,所以
,所以 在
在 上是减函数,故
上是减函数,故 .
.
综上所述: 时,
时,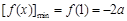
 时,
时,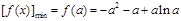
 时,
时,
(2)令
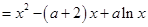

由

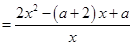
 ,解得;
,解得;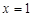 或
或
由 , 知
, 知
故当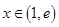 时,
时, ,则
,则 在
在 上是增函数
上是增函数
又 ;
;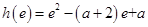


由已知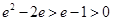 得:
得: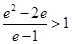 ,所以
,所以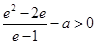 ,所以
,所以
故函数 在
在 上有唯一的零点,即方程
上有唯一的零点,即方程 在区间<
在区间<

练习册系列答案
相关题目
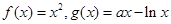 ,
,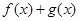 在
在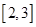 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;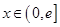 (
(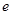 是自然常数)时,函数
是自然常数)时,函数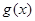 的最小值是3,若存在,求出
的最小值是3,若存在,求出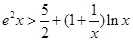 .
. .
. 的解集;
的解集;
 ,若
,若 对任意的
对任意的 都成立,求
都成立,求 的取值范围.
的取值范围.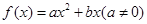 满足条件:①
满足条件:①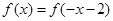 ;②函数
;②函数 的图像与直线
的图像与直线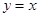 相切.
相切.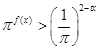 在
在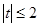 时恒成立,求实数
时恒成立,求实数 的取值范围.
的取值范围. 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.

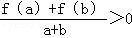 .
.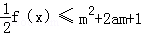 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
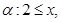 命题
命题 且命题
且命题 是
是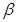 的必要条件,求实数m的取值范围
的必要条件,求实数m的取值范围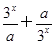 是R上的偶函数.
是R上的偶函数.