题目内容
已知函数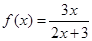 ,数列
,数列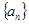 满足
满足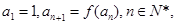
(I)求证:数列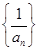 是等差数列;
是等差数列;
(II)令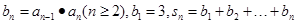 ,若
,若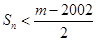 对一切
对一切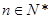 成立,求最小正整数
成立,求最小正整数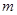 .
.
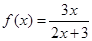 ,数列
,数列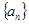 满足
满足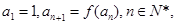
(I)求证:数列
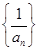 是等差数列;
是等差数列;(II)令
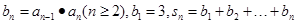 ,若
,若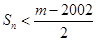 对一切
对一切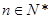 成立,求最小正整数
成立,求最小正整数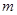 .
.(1)证明:由题意可得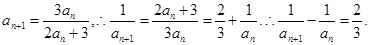
又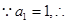 数列
数列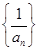 是以
是以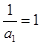 为首项,以
为首项,以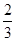 为公差的等差数列.
为公差的等差数列.
(2)由(1)可得
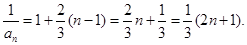
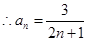 当
当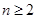 时,
时,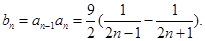
当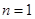 时,上式同样成立。
时,上式同样成立。
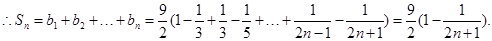
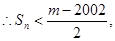 即
即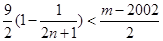 对一切
对一切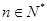 成立,
成立,
又 随
随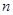 递增,且
递增,且
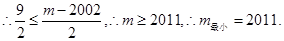
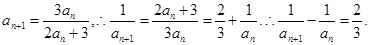

又
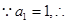 数列
数列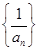 是以
是以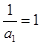 为首项,以
为首项,以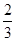 为公差的等差数列.
为公差的等差数列.(2)由(1)可得

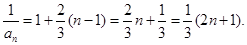
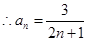 当
当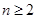 时,
时,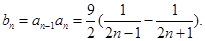
当
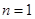 时,上式同样成立。
时,上式同样成立。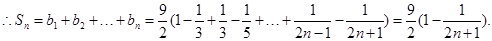
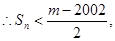 即
即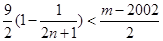 对一切
对一切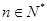 成立,
成立,又
 随
随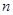 递增,且
递增,且
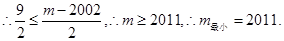
略

练习册系列答案
相关题目
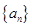 为等差数列,则下列数列中,成等差数列的个数为( )
为等差数列,则下列数列中,成等差数列的个数为( )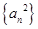 ②
② ③
③ ④
④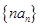 (p、q为非零常数)
(p、q为非零常数) 中,
中, ,
, 是其前
是其前 项和,且
项和,且 .
.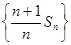 是等差数列;
是等差数列; ,记数列
,记数列 的前
的前 .
. 时,
时,

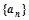 是公比大于1的等比数列,Sn为数列
是公比大于1的等比数列,Sn为数列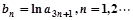 ,求数列
,求数列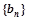 的前n项和Tn.
的前n项和Tn. ,数列
,数列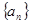 满足
满足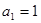 ,
,
 ;
;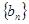 满足
满足 …+
…+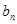 ,求
,求 .
.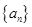 为等差数列,
为等差数列,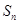 为其前
为其前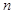 项和,且
项和,且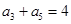 ,则
,则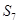 等于( )
等于( )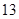
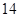
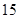
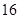
 中,若
中,若 ,则
,则 ;
; 的前
的前 项和
项和 是实数),下列结论正确的是 ( )
是实数),下列结论正确的是 ( ) 为任意实数,
为任意实数, 均是等比数列
均是等比数列 时,
时, 时,
时, 时,
时,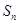 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则  ________
________