题目内容
4.在下列各题中,试判断p是q的什么条件.(1)p:$\frac{1}{x}<$1,q:x>1;
(2)p:b=0,q:函数y=ax2+bx+c是偶函数;
(3)p:k>0,q:函数y=$\frac{k}{x}$在(-∞,0)上和(0,+∞)上是减函数;
(4)p:平行四边形的对角线相等,q:这个平行四边形是矩形.
分析 结合充要条件的定义,逐一分析给定的条件p与条件q的关系,可得结论.
解答 解:(1)p:$\frac{1}{x}<$1?x<0,或x>1,q:x>1,故p是q的必要不充分条件;
(2)b=0时函数y=ax2+c是偶函数,函数y=ax2+bx+c是偶函数时,b=0,则p是q的充要条件;
(3)k>0时,函数y=$\frac{k}{x}$在(-∞,0)上和(0,+∞)上是减函数,
函数y=$\frac{k}{x}$在(-∞,0)上和(0,+∞)上是减函数时,k>0,则p是q的充要条件;
(4)平行四边形的对角线相等时,这个平行四边形是矩形.
平行四边形是矩时,对角线相等,则p是q的充要条件;
点评 本题考查的知识点是充要条件的定义,熟练掌握并正确理解充要条件的定义是解答的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程是3x±4y=0,则此双曲线的离心率是( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
19.对于正实数a,函数y=x+$\frac{a}{x}$在($\frac{3}{4}$,+∞)上为增函数,则a的取值范围为 ( )
| A. | ($\frac{2}{3}$,+∞) | B. | (0,$\frac{9}{16}$] | C. | (0.+∞) | D. | ($\frac{9}{16}$,+∞) |
16.化简$\frac{{x}^{2}{x}^{-3}{x}^{\frac{2}{3}}}{{x}^{\frac{1}{3}}{x}^{-2}{x}^{-\frac{8}{3}}}$的结果是 ( )
| A. | x${\;}^{\frac{4}{3}}$ | B. | x2 | C. | x3 | D. | x4 |
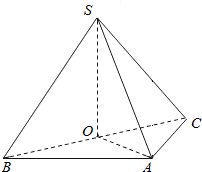 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.