题目内容
.已知实数 ,则M的最小值为( )
,则M的最小值为( )
A. | B.2 | C.4 | D.1 |
A
解析试题分析:因为 ,那么根据均值不等式的结论,可知
,那么根据均值不等式的结论,可知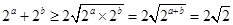 ,因此可知M的最小值为
,因此可知M的最小值为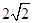 ,故选A.
,故选A.
考点:本题主要考查均值不等式的求解最值问题的运用。
点评:解决该试题的关键是利用和为定值,则积有最大值,可知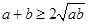 ,那么得到M的最小值的求解问题。
,那么得到M的最小值的求解问题。

练习册系列答案
相关题目
设x>0,y>0,x+y+xy=2,则x+y的最小值是( )
A.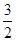 | B.1 + 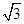 | C.2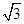 -2 -2 | D.2-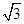 |
已知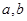 是不相等的正数,且
是不相等的正数,且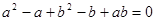 ,则
,则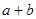 的取值范围是
的取值范围是
A.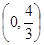 | B.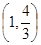 | C. | D.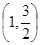 |
设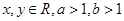 ,若
,若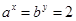 ,
,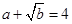 ,则
,则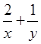 的最大值为( )
的最大值为( )
| A.3 | B.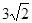 | C.4 | D.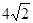 |
下列命题中正确的是 ( )
A. 的最小值是2 的最小值是2 | B. 的最小值是2 的最小值是2 |
C. 的最小值是 的最小值是 | D. 的最大值是 的最大值是 |
设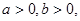 则以下不等式中不恒成立的是
则以下不等式中不恒成立的是
A.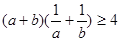 | B.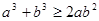 |
C. | D.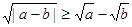 |
对于使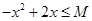 成立的所有常数
成立的所有常数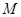 中,我们把
中,我们把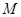 的最小值
的最小值 叫做
叫做 的上确界,若
的上确界,若 ,则
,则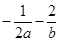 的上确界为 ( )
的上确界为 ( )
| A.-3 | B. | C.- | D. |
当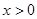 时,下列函数中最小值为2的是( )
时,下列函数中最小值为2的是( )
A.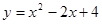 | B.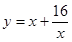 |
C. | D.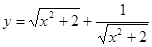 |
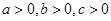 ,若
,若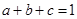 ,则
,则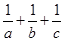 的最小值为____________.
的最小值为____________.