题目内容
【题目】如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).
(1)求抛物线C的方程及准线l的方程;
(2)过焦点F的直线(不经过Q点)与抛物线交于A,B两点,与准线l交于点M,记QA,QB,QM的斜率分别为k1 , k2 , k3 , 问是否存在常数λ,使得k1+k2=λk3成立?若存在λ,求出λ的值;若不存在,说明理由.
【答案】
(1)
解:把Q(1,2)代入y2=2px,得2p=4,所以抛物线方程为y2=4x,
准线l的方程为x=﹣1
(2)
解:由条件可设直线AB的方程为y=k(x﹣1),k≠0.
由抛物线准线l:x=﹣1,可知M(﹣1,﹣2k),又Q(1,2),所以 ![]() ,
,
把直线AB的方程y=k(x﹣1),代入抛物线方程y2=4x,并整理,可得k2x2﹣2(k2+2)x+k2=0,设A(x1,y1),B(x2,y2),则 ![]() ,
,
又Q(1,2),故 ![]() .因为A,F,B三点共线,所以kAF=kBF=k,
.因为A,F,B三点共线,所以kAF=kBF=k,
即 ![]() ,
,
所以 ![]() ,
,
即存在常数λ=2,使得k1+k2=2k3成立
【解析】(1)把Q(1,2)代入y2=2px,得2p=4,即可求抛物线C的方程及准线l的方程;(2)把直线AB的方程y=k(x﹣1),代入抛物线方程y2=4x,并整理,求出k1+k2 , k3 , 即可得出结论.

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如表频数表: 甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
(Ⅰ)现从甲公司记录的100天中随机抽取两天,求这两天送餐单数都大于40的概率;
(Ⅱ)若将频率视为概率,回答下列问题:
(i)记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
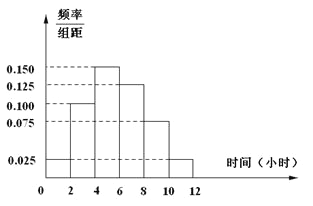
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
