Question

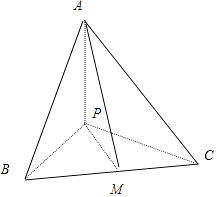
【题目】三棱锥P﹣ABC中，PA、PB、PC互相垂直，PA=PB=1，M是线段BC上一动点，若直线AM与平面PBC所成角的正切的最大值是 ，则三棱锥P﹣ABC的外接球的表面积是（ ）
A.2π
B.4π
C.8π
D.16π

Answer 1

【答案】B
【解析】解：M是线段BC上一动点，连接PM，∵PA、PB、PC互相垂直，∴∠AMP就是直线AM与平面PBC所成角，

当PM最短时，即PM⊥BC时直线AM与平面PBC所成角的正切的最大．

此时 ，PM= ，

在Rt△PBC中，PBPC=BCPMPC= PC= ．

三棱锥P﹣ABC扩充为长方体，则长方体的对角线长为 ，

∴三棱锥P﹣ABC的外接球的半径为R=1，

∴三棱锥P﹣ABC的外接球的表面积为4πR2=4π．

故选：B．