题目内容
11.求函数f(t)=$\sqrt{1-t}$+$\sqrt{t}$在[-1,1]上的最大值和最小值.分析 由题意,0≤t≤1,设t=sin2α,α∈[0,$\frac{π}{2}$],则y=cosα+sinα=$\sqrt{2}$sin(α+$\frac{π}{4}$),利用三角函数的图象即可得出结论.
解答 解:由题意,0≤t≤1,设t=sin2α,α∈[0,$\frac{π}{2}$],则
y=cosα+sinα=$\sqrt{2}$sin(α+$\frac{π}{4}$)
∵α∈[0,$\frac{π}{2}$],∴α+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{3π}{4}$],
∴sin(α+$\frac{π}{4}$)∈[$\frac{\sqrt{2}}{2}$,1],
∴y∈[1,$\sqrt{2}$],
∴函数f(t)=$\sqrt{1-t}$+$\sqrt{t}$在[-1,1]上的最大值为$\sqrt{2}$,最小值为1.
点评 本题考查函数的最值,考查学生分析转化问题的能力,正确换元是关键.

练习册系列答案
相关题目
3.三棱锥P-ABC中,D、E分别为PB、PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,则V1:V2=( )
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
1.在△ABC中,sinA:sinB:sinC=3:2:3,则cosC的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
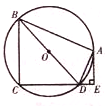 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE,与CD的延长线交于E,AE⊥CD,垂足为点E.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE,与CD的延长线交于E,AE⊥CD,垂足为点E.