题目内容
 如图,直角三角形ABC的顶点A的坐标为(-1,0),直角顶点B的坐标为(0,-
如图,直角三角形ABC的顶点A的坐标为(-1,0),直角顶点B的坐标为(0,-| 3 |
(1)求点C的坐标及△ABC的外接圆M的方程;
(2)设△ABC的外接圆M的圆心为点M,另有一个定点N(-3,-4),作出一个以MN为直径,G为圆心的圆,记为圆G,圆M和圆G交于点P和点Q,直线NP,NQ是圆M的切线吗?请说明理由;
(3)求直线PQ的方程.
分析:(1)求出直线BC的方程,可得点C的坐标,根据△ABC为直角三角形,确定△ABC的外接圆M的圆心与半径,从而可求方程;
(2)求出圆G的方程,利用切线的定义,即可得到结论;
(3)两圆方程相减,可得直线PQ的方程.
(2)求出圆G的方程,利用切线的定义,即可得到结论;
(3)两圆方程相减,可得直线PQ的方程.
解答:解:(1)由题意可知:kAB=-
,∴kBC=
,
直线BC的方程为:y+
=
(x-0),令y=0,则x=3,所以点C的坐标为(3,0),
∵△ABC为直角三角形,∴△ABC外接圆的圆心为线段AC的中点M(1,0),半径为
|AC|=2,
∴圆M的方程为:(x-1)2+y2=4;
(2)∵M(1,0),N(-3,-4)
∴线段MN的中点为G(-1,-2),|MN|=4
∴圆G的方程为:(x+1)2+(y+2)2=8
∵MN为圆G的直径,P,Q为圆G上的点
∴PM⊥PN,QM⊥QN
∴直线NP,NQ是圆M的切线;
(3)∵圆M的方程为:(x-1)2+y2=4,圆G的方程为:(x+1)2+(y+2)2=8,
∴两圆方程相减,可得直线PQ的方程为x+y=0.
| 3 |
| ||
| 3 |
直线BC的方程为:y+
| 3 |
| ||
| 3 |
∵△ABC为直角三角形,∴△ABC外接圆的圆心为线段AC的中点M(1,0),半径为
| 1 |
| 2 |
∴圆M的方程为:(x-1)2+y2=4;
(2)∵M(1,0),N(-3,-4)
∴线段MN的中点为G(-1,-2),|MN|=4
| 2 |
∴圆G的方程为:(x+1)2+(y+2)2=8
∵MN为圆G的直径,P,Q为圆G上的点
∴PM⊥PN,QM⊥QN
∴直线NP,NQ是圆M的切线;
(3)∵圆M的方程为:(x-1)2+y2=4,圆G的方程为:(x+1)2+(y+2)2=8,
∴两圆方程相减,可得直线PQ的方程为x+y=0.
点评:本题考查圆的方程,考查直线与圆、圆与圆的位置关系,属于中档题.

练习册系列答案
相关题目
 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=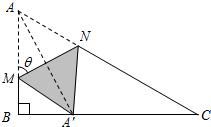 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC= (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答) (2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)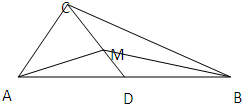 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.