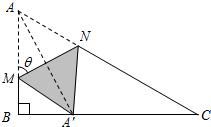
题目内容
 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=| 3 |
(1)用θ表示∠BA′M和线段AM的长度,并写出θ的取值范围;
(2)求线段AN长度的最小值.
分析:(1)由折叠可知△AMN≌△A′MN,可得对应角相等,∠AMN=θ,可得出∠A′MA=2θ,在直角三角形A′MB,根据直角三角形的两锐角互余,即可表示∠BA′M,设MA=MA′=x,由AB=1,利用AB-AM表示出MB为1-x,Rt△MBA′中,根据锐角三角函数定义用x表示出sin(2θ-90°),求出x,利用诱导公式及二倍角的正弦函数公式化简,即可表示出MA,同时由点M在线段AB上,M点和B点不重合,A′点和B点不重合,可得出θ的取值范围;
(2)在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,可得出AC=2AB,即∠ACB为30°,得出∠BAC为60°,在三角形AMN中,∠AMN=θ,利用三角形内角和定理表示出∠ANM,再由AM的长,利用正弦定理列出关系式,化简可得出AN=
,设t=2sinθsin(120°-θ),利用两角和与差的正弦函数公式及特殊角的三角函数值化简,去括号后再利用二倍角的正弦、余弦函数公式变形,再利用两角和与差的正弦函数公式化为一个角的正弦函数,由θ的范围求出这个角的范围,根据正弦函数的图象与性质得到此时正弦函数的值域,可得出t的最大值,进而确定出AN的最小值.
(2)在直角三角形ABC中,由AB及BC的长,利用勾股定理求出AC的长,可得出AC=2AB,即∠ACB为30°,得出∠BAC为60°,在三角形AMN中,∠AMN=θ,利用三角形内角和定理表示出∠ANM,再由AM的长,利用正弦定理列出关系式,化简可得出AN=
| 1 |
| 2sinθsin(120°-θ) |
解答:解:(1)易知△AMN≌△A′MN,∴∠A′MA=2θ,
则∠A′MB=180°-2θ,∠BA′M=90°-(180°-2θ)=2θ-90°,(2分)
设MA=MA′=x,则MB=1-x,
在Rt△MBA′中,sin(2θ-90°)=-cos2θ=
,
∴MA=x=
=
,(5分)
∵点M在线段AB上,M点和B点不重合,A′点和B点不重合,
∴45°<θ<90°;(6分)
(2)∵∠B=90°,AB=1,BC=
,
∴根据勾股定理得:AC=2,
∴∠BAC=60°,
在△AMN中,由∠AMN=θ,可得∠ANM=180°-60°-θ=120°-θ,
又MA=
,
∴根据正弦定理得:
=
,
可得:AN=
=
,(8分)
令t=2sinθsin(120°-θ)=2sinθ(
sinθ+
cosθ)
=sin2θ+
sinθcosθ=
+
sin2θ-
cos2θ=
+sin(2θ-30°),(11分)
∵45°<θ<90°,∴60°<2θ-30°<150°,
当且仅当2θ-30°=90°,θ=60°时,t有最大值
,
则θ=60°时,AN有最小值
.(13分)
则∠A′MB=180°-2θ,∠BA′M=90°-(180°-2θ)=2θ-90°,(2分)
设MA=MA′=x,则MB=1-x,
在Rt△MBA′中,sin(2θ-90°)=-cos2θ=
| 1-x |
| x |
∴MA=x=
| 1 |
| 1-cos2θ |
| 1 |
| 2sin2θ |
∵点M在线段AB上,M点和B点不重合,A′点和B点不重合,
∴45°<θ<90°;(6分)
(2)∵∠B=90°,AB=1,BC=
| 3 |
∴根据勾股定理得:AC=2,
∴∠BAC=60°,
在△AMN中,由∠AMN=θ,可得∠ANM=180°-60°-θ=120°-θ,
又MA=
| 1 |
| 2sin2θ |
∴根据正弦定理得:
| AN |
| sinθ |
| MA |
| sin(120°-θ) |
可得:AN=
sinθ×
| ||
| sin(120°-θ) |
| 1 |
| 2sinθsin(120°-θ) |
令t=2sinθsin(120°-θ)=2sinθ(
| 1 |
| 2 |
| ||
| 2 |
=sin2θ+
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵45°<θ<90°,∴60°<2θ-30°<150°,
当且仅当2θ-30°=90°,θ=60°时,t有最大值
| 3 |
| 2 |
则θ=60°时,AN有最小值
| 2 |
| 3 |
点评:此题考查了正弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,正弦函数的定义域与值域,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC= (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答) (2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分) 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.