题目内容
【题目】已知函数![]() 与函数
与函数![]() 的图像关于直线
的图像关于直线![]() 对称,函数
对称,函数![]()
![]() .
.
(Ⅰ)若![]() ,且关于
,且关于![]() 的方程
的方程![]() 有且仅有一个解,求实数
有且仅有一个解,求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,若关于
时,若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析: ∵函数![]() 与函数
与函数![]() 的图像关于直线
的图像关于直线![]() 对称,∴
对称,∴![]() ,
,
∴![]()
(Ⅰ)令![]() ,则
,则![]() ,即
,即![]()
令![]() ,利用导数研究
,利用导数研究 ![]() 的性质,可得
的性质,可得![]() ,
,
又![]() ,
, ![]() ,
, ![]() 所以当函数
所以当函数![]() 有且仅有一个零点时,
有且仅有一个零点时, ![]() .
.
(Ⅱ)当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() ,
,
利用导数研究 ![]() 的性质,可得
的性质,可得![]() 是
是![]() 的极大值点.
的极大值点.
∵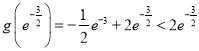
![]()
∴![]() ,即可求出实数
,即可求出实数![]() 的取值范围.
的取值范围.
试题解析:∵函数![]() 与函数
与函数![]() 的图像关于直线
的图像关于直线![]() 对称,∴
对称,∴![]() ,
,
∴![]()
(Ⅰ)令![]() ,则
,则![]() ,即
,即![]()
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() 所以
所以![]() 在
在![]() 上是减函数,
上是减函数,
又![]() ,所以当
,所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
又![]() ,
, ![]() ,
, ![]()
所以当函数![]() 有且仅有一个零点时,
有且仅有一个零点时, ![]() ,∴
,∴![]() .
.
(Ⅱ)当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() ,
,
易知,当![]() 时,
时, ![]() 恒成立,等价于
恒成立,等价于![]() .
.
因为![]() ,令
,令![]() 得
得![]() ,或
,或![]()
又![]() ,所以函数
,所以函数![]() 在
在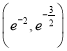 上单调递增,在
上单调递增,在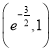 上单调递减,在
上单调递减,在![]() 上单调递增,即
上单调递增,即![]() 是
是![]() 的极大值点.
的极大值点.
∵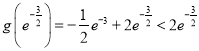
![]()
∴![]() ,即
,即![]() 为所求.
为所求.

【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | 50 |
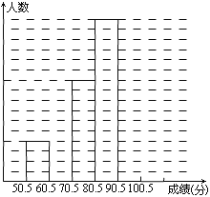
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
【题目】编号分别为![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(1)将得分在对应区间内的人数填入相应的空格:
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(2)从得分在区间[20,30)内的运动员中随机抽取2人.
(ⅰ)用运动员编号列出所有可能的抽取结果;
(ⅱ)求这2人得分之和大于50的概率.
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 | 400 | 300 | 700 |
认为共享产品对生活无益 | 100 | 200 | 300 |
总计 | 500 | 500 | 1000 |
(1)根据表中的数据,能否在犯错误的概率不超过0.1%的前提下,认为共享产品的态度与性别有关系?
(2)为了答谢参与问卷调查的人员,该公司对参与本次问卷调查的人员随机发放1张超市的购物券,购物券金额以及发放的概率如下:
购物券金额 | 20元 | 50元 |
概率 |
|
|
现有甲、乙两人领取了购物券,记两人领取的购物券的总金额为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: 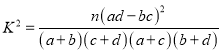 .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


