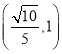题目内容
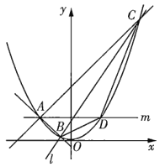
【题目】已知抛物线![]() :
:![]() 的准线经过点
的准线经过点![]() ,过
,过![]() 的焦点
的焦点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,则下列结论正确的是( )
两点,则下列结论正确的是( )
A.![]() B.
B.![]() 的最小值为16
的最小值为16
C.四边形![]() 的面积的最小值为64D.若直线
的面积的最小值为64D.若直线![]() 的斜率为2,则
的斜率为2,则![]()
【答案】ABD
【解析】
由准线的概念可得![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() 得直线
得直线![]() 的方程,与抛物线方程联立方程组消元后,应用韦达定理得
的方程,与抛物线方程联立方程组消元后,应用韦达定理得![]() ,由抛物线焦点弦长公式可得
,由抛物线焦点弦长公式可得![]() ,直线
,直线![]() 斜率为
斜率为![]() ,同理可得
,同理可得![]() ,利用基本不等式可判断B,C,计算
,利用基本不等式可判断B,C,计算![]() ,代入
,代入![]() 可判断D.
可判断D.
由题可知![]() ,所以
,所以![]() ,故A正确.
,故A正确.
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() .设
.设![]() ,
,![]() ,
,
![]() ,
,![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() .联立
.联立
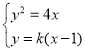 ,消去
,消去![]() 整理得
整理得![]() ,所以
,所以![]() ,
,
![]() .所以
.所以![]() .
.
同理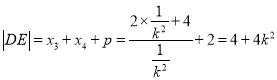 ,
,
从而![]() ,当且仅当
,当且仅当![]() 时等号成立,故B正确.
时等号成立,故B正确.
因为![]()
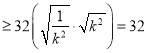 ,
,
当且仅当![]() 时等号成立,故C错误.
时等号成立,故C错误.
![]()
![]() ,将
,将
![]() ,
,![]() 与
与![]() ,
,![]() 代入上式,得
代入上式,得![]() ,所以
,所以![]() ,故D正确.
,故D正确.
故选:ABD.

练习册系列答案
相关题目