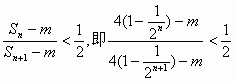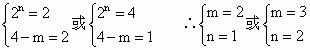Question

解答题：解答时要求写出必要的文字说明或推演步骤． 已知数列{an}的前n项和Sn满足Sn+1＝KSn＋2，又a1＝2，a2＝1． (1) 求k的值 (2) 求Sn (3) 已知存在正整数m、n，使成立，试求出m、n的值．

Answer 1

答案：
解析：

(1)	解：∵S2＝KS1＋2∴a1＋a2＝Ka1＋2．又a1＝2，a2＝1，∴K＝……………2′
(2)	解：　　　　①n≥2时，Sn＝Sn－1＋2　　　　②， ①－②得……………………………………………………4′ 又a2＝a1，an≠0(n∈N*)是等比数列，公比为 ………………………………………………7′
(3)	解：不等式 整理得……………………9′ ∵存在正整数m，n使得上面的不等式成立，由于2n为整数，4－m为整数， 则只能2n(4－m)＝4…………………………………………………………10′ ∴ 即m＝2，n＝1或m＝3，n＝2．……………………………………………………12′