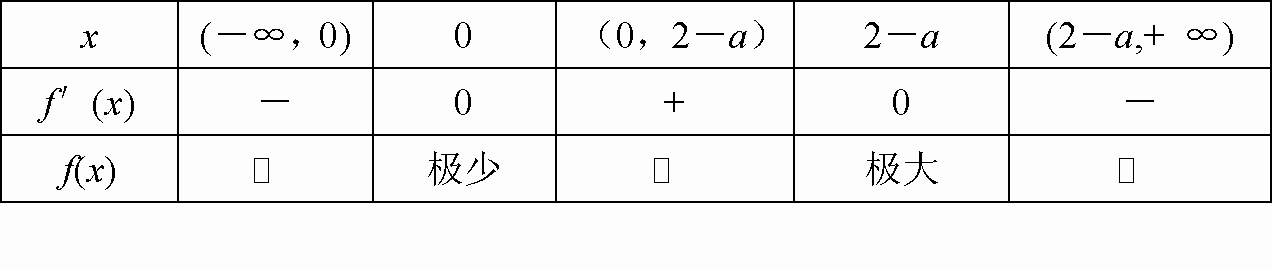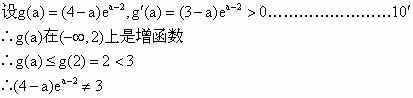题目内容
| |||||||||||
答案：
解析：
解析：
(1) |
解：当
∴f(x)的单调递增区间为(0，1)，单调递减区间(－∞，0)(1，＋∞)…4′ |
(2) |
解： 令 列表如下：
由表可知，
∴不存在实数a，使f(x)最大值为3．…………………………………………12′ |
……2′
………………6′
……………………………………8′
练习册系列答案
相关题目
与
的夹角θ
| |||||||||||
成立，试求出m、n的值．
＝(1，0)，
＝(0，1)，规定
＝x(x－1)……(x－m＋1)，其中x∈R，m∈N+，且
＝1．函数f(x)＝
(ab≠0)在x＝1处取得极值，在x＝2处的切线平行向量
＝(b＋5，5a)．
在区间(m，m＋1)内有且只有两个不等实根？若存在，求出m的值；若不存在，说明理由．