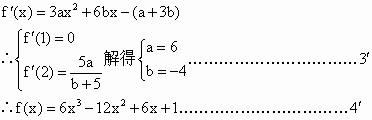题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:由已知
|
(2) |
解:
|
(3) |
解:方程 令g(x)=18x3-36x2+19………………………………………………9′
∴方程g(x)=0在区间(1, ∴存在正整数m=1使得方程 |

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
| |||||||||||