题目内容
如图,在长方体 中,
中, ,
, ,
, 分别是面
分别是面 ,面
,面 的中心,则
的中心,则 和
和 所成的角为( )
所成的角为( )

 中,
中, ,
, ,
, 分别是面
分别是面 ,面
,面 的中心,则
的中心,则 和
和 所成的角为( )
所成的角为( )
A. | B. | C. | D. |
D
试题分析:以D为坐标原点,
 分别为
分别为 轴建立空间直角坐标系,则根据题目所给数据可知
轴建立空间直角坐标系,则根据题目所给数据可知 ,
,则
 ,
, ,
,所以
 ,所以
,所以 和
和 所成的角为
所成的角为 .
.点评:求解两条异面直线所成的角,可以先通过作平行线作出两条异面直线所成的角,也可以建立空间直角坐标系利用空间向量解决.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
 中,对角线
中,对角线 于
于 ,
, ,
, 为
为 的重心,过点
的重心,过点 分别交
分别交 于
于 且
且 ,沿
,沿 将
将 折起,沿
折起,沿 折起,
折起, 正好重合于
正好重合于 .
. 
 平面
平面 ;
;  与平面
与平面 夹角的大小.
夹角的大小.  ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题: ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ;
; ,
, ,
, ;④ 若
;④ 若 ,
, ,
, 中,
中, 分别是
分别是 ,
,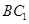 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )
 与
与 垂直
垂直 垂直
垂直 异面
异面 异面
异面 中,平面
中,平面 ∥平面
∥平面 ,
, ⊥平面
⊥平面 ,
, ,
,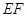 ∥
∥ .
. ,
,  .
.
 平面
平面 ;
; ∥平面
∥平面 ;
; 的余弦值.
的余弦值. 和两条不重合的直线m,n,则下列四种说法正确的为( )
和两条不重合的直线m,n,则下列四种说法正确的为( ) α,则m∥α
α,则m∥α 、
、 是不同的直线,
是不同的直线, 、
、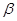 、
、 是不同的平面,有以下四命题:
是不同的平面,有以下四命题:  ,则
,则 ; ②若
; ②若 ,则
,则 ;
; ,则
,则 ; ④若
; ④若 ,则
,则 .
. 的底面为菱形,且
的底面为菱形,且 ,
,
 ,
, 为
为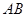 的中点.
的中点.

 平面
平面 ;
; 到面
到面 的距离.
的距离. 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
.