题目内容
【题目】已知函数f(x)=(x﹣1)lnx﹣(x﹣a)2(a∈R). (Ⅰ)若f(x)在(0,+∞)上单调递减,求a的取值范围;
(Ⅱ)若f(x)有两个极值点x1 , x2 , 求证:x1+x2> ![]() .
.
【答案】解:(Ⅰ)由已知, ![]() 恒成立
恒成立
令 ![]() ,则
,则 ![]() ,
,
﹣(2x+1)<0,令g′(x)>0,解得:0<x<1,令g′(x)<0,解得:x>1,
故g(x)在(0,1)递增,在(1,+∞)递减,
∴g(x)max=g(1)=2a﹣2∴由f'(x)≤0恒成立可得a≤1.
即当f(x)在(0,+∞)上单调递减时,a的取值范围是(﹣∞,1].
(Ⅱ)若f(x)有两个极值点x1,x2,不妨设0<x1<x2.
由(Ⅰ)可知a>1,且f′(x1)=lnx1﹣ ![]() ﹣2x1+1+2a①,f′(x2)=lnx2﹣
﹣2x1+1+2a①,f′(x2)=lnx2﹣ ![]() ﹣2x2+1+2a②,
﹣2x2+1+2a②,
由①﹣②得: ![]() ∴
∴ 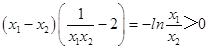 ∴
∴ ![]() ,即
,即 ![]() ,
,
由①+②得: ![]() ,
,
∴ 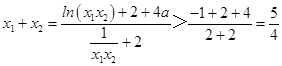
【解析】(Ⅰ)求出函数的导数,得到f′(x)≤0恒成立,令 ![]() ,求出函数的导数,根据函数的单调性得到g(x)max≤0,求出a的范围即可;(Ⅱ)根据f′(x1)=lnx1﹣
,求出函数的导数,根据函数的单调性得到g(x)max≤0,求出a的范围即可;(Ⅱ)根据f′(x1)=lnx1﹣ ![]() ﹣2x1+1+2a①,f′(x2)=lnx2﹣
﹣2x1+1+2a①,f′(x2)=lnx2﹣ ![]() ﹣2x2+1+2a②,得到:x1+x2的解析式,从而证明结论即可.
﹣2x2+1+2a②,得到:x1+x2的解析式,从而证明结论即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
【题目】2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛MVP(最有价值球员),如表是易建联在这9场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国91﹣42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
中国76﹣73韩国 | 7/13 | 6/8 | 20 | 60.53% |
中国84﹣67约旦 | 12/20 | 2/5 | 26 | 58.56% |
中国75﹣62哈萨克期坦 | 5/7 | 5/5 | 15 | 81.52% |
中国90﹣72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
中国85﹣69卡塔尔 | 4/10 | 4/4 | 13 | 55.27% |
中国104﹣58印度 | 8/12 | 5/5 | 21 | 73.94% |
中国70﹣57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
中国78﹣67菲律宾 | 4/14 | 3/6 | 11 | 33.05% |
注:①表中a/b表示出手b次命中a次;
②TS%(真实得分率)是衡量球员进攻的效率,其计算公式为:
TS%= ![]() .
.
(Ⅰ)从上述9场比赛中随机选择一场,求易建联在该场比赛中TS%超过50%的概率;
(Ⅱ)从上述9场比赛中随机选择两场,求易建联在这两场比赛中TS%至少有一场超过60%的概率;
(Ⅲ)用x来表示易建联某场的得分,用y来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断y与x之间是否具有线性相关关系?结合实际简单说明理由.