Question

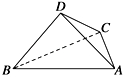
【题目】如图，多面体ABCDE中，AB=AC，平面BCDE⊥平面ABC，BE∥CD，CD⊥BC，BE=1，BC=2，CD=3，M为BC的中点．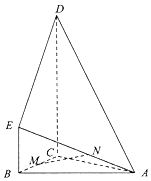
（1）若N是棱AE上的动点，求证：DE⊥MN；
（2）若平面ADE与平面ABC所成锐二面角为60°，求棱AB的长．

Answer 1

【答案】
（1）证明：连结EM、AM、DM，

∵AB=AC，且M为BC的中点，∴AM⊥BC，

∵平面BCDE⊥平面ABC，∴AM⊥平面BCDE，∴AM⊥DE，

∵在直角梯形BCDE中，BE=1，BC=2，CD=3，

∴△DEM中，DE=2 ，EM= ，DM= ，

∴DE2+EM2=DM2，∴DE⊥EM，

又AM∩EM=M，∴DE⊥平面AEM，

∵MN平面AEM，∴DE⊥MN．

（2）解：取DE的中点P，则PM∥BE，

∵BE⊥BC，∴PM⊥BC，由（1）知，AM⊥平面BCDE，

∴MB、MA、MP两两垂直，如图，建立空间直角坐标系M﹣xyz，

设AM=t，（t＞0），则A（0，t，0），D（﹣1，0，3），E（1，0，1），

∴ =（﹣1，﹣t，3）， =（2，0，﹣2），

设平面ADE的一个法向量为 =（x，y，z），

则 ，令x=t，则 =（t，2，t），

∵平面ABC的一个法向量 =（0，0，1），

∵二面角A﹣DE﹣B为60°，

∴|cos60°|=|cos＜ ＞|=| |= ，

解得t= ，此时AB= ．

【解析】（1）连结EM、AM、DM，推导出AM⊥DE，DE⊥EM，从而DE平面AEM，由此能证明DE⊥MN．（2）取DE的中点P，建立空间直角坐标系M﹣xyz，利用向量法能求出结果．
【考点精析】关于本题考查的空间中直线与直线之间的位置关系，需要了解相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点才能得出正确答案．