题目内容
已知函数f(x)的图象与函数g(x)=1+2lgx(x>0)的图象关于直线y=x对称,则函数f(x)的图象与y轴的交点坐标是
- A.
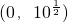
- B.
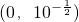
- C.(0,102)
- D.(0,10-2)
B
分析:由两个函数的图象关于直线y=x对称得,这两个函数互为反函数,故只要利用求反函数的方法求出原函数的反函数,最后求出函数f(x)的图象与y轴的交点坐标.
解答:∵函数y=g(x)=1+2lgx(x>0)的图象与函数f(x)的图象关于直线y=x对称,
∴函数y=g(x)=1+2lgx(x>0)与函数f(x)互为反函数,
又∵函数g(x)=1+2lgx(x>0)的反函数为:y=10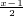 ,
,
即f(x)=10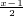 ,
,
∴f(0)=10 =
=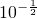 ,
,
则函数f(x)的图象与y轴的交点坐标是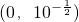
故选B.
点评:本小题主要考查反函数、对数式的运算等基础知识,考查运算求解能力、化归与转化思想.属于基础题.
分析:由两个函数的图象关于直线y=x对称得,这两个函数互为反函数,故只要利用求反函数的方法求出原函数的反函数,最后求出函数f(x)的图象与y轴的交点坐标.
解答:∵函数y=g(x)=1+2lgx(x>0)的图象与函数f(x)的图象关于直线y=x对称,
∴函数y=g(x)=1+2lgx(x>0)与函数f(x)互为反函数,
又∵函数g(x)=1+2lgx(x>0)的反函数为:y=10
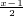 ,
,即f(x)=10
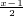 ,
,∴f(0)=10
 =
=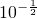 ,
,则函数f(x)的图象与y轴的交点坐标是
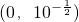
故选B.
点评:本小题主要考查反函数、对数式的运算等基础知识,考查运算求解能力、化归与转化思想.属于基础题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(