题目内容
【题目】已知p:x2≤5x-4,q:x2-(a+2)x+2a≤0.
(1)若p是真命题,求对应x的取值范围;
(2)若p是q的必要不充分条件,求a的取值范围.
【答案】(1)x的取值范围为[1,4](2)a的取值范围为[1,4]
【解析】
(1)根据一元二次不等式的解法,即可求命题![]() 中对应
中对应![]() 的范围;
的范围;
(2)利用![]() 是
是![]() 的必要不充分条件,建立条件关系,即可求
的必要不充分条件,建立条件关系,即可求![]() 的取值范围.
的取值范围.
1)因为x2≤5x-4,
所以x2-5x+4≤0,
即(x-1)(x-4)≤0,所以1≤x≤4,
即对应x的取值范围为[1,4].
(2)设p对应的集合为A={x|1≤x≤4}.
由x2-(a+2)x+2a≤0,
得(x-2)(x-a)≤0.
当a=2时,不等式的解为x=2,对应的解集为B={2};
当a>2时,不等式的解为2≤x≤a,对应的解集为B={x|2≤x≤a};
当a<2时,不等式的解为a≤x≤2,对应的解集为B={x|a≤x≤2}.
若p是q的必要不充分条件,则BA,
当a=2时,满足条件;
当a>2时,因为A={x|1≤x≤4},
B={x|2≤x≤a},
要使BA,则满足2<a≤4;
当a<2时,因为A={x|1≤x≤4},B={x|a≤x≤2},要使BA,则满足1≤a<2.
综上,a的取值范围为[1,4].

 优生乐园系列答案
优生乐园系列答案【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: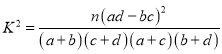 (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |