题目内容
13．
某人设计了一个图案如图所示，他有四个颜色想都涂在这个图案的六个区域中，相邻不能同色（如①②为相邻，①⑤为不相邻等），他有（ ）种涂色方法．| A． | 408 | B． | 336 | C． | 360 | D． | 384 |
分析 分类讨论，利用乘法原理，即可得出结论．
解答 解：①⑤同色，有4种方法，②、④同色，有3种方法，③⑥有2种方法，共有4×3×2=24种方法；
①⑤同色，有4种方法，②、④不同色，有3×2种方法，③⑥有4种方法，共有4×3×2×4=96种方法；
①⑤不同色，有4×3种方法，②、④同色，有2种方法，③⑥有4种方法，共有4×3×2×4=96种方法；
①⑤不同色，有4×3种方法，②、④不同色，有2种方法，③⑥有5种方法，共有4×3×2×5=216种方法；
故共有336种方法，
故选：B．
点评 本题考查乘法原理，考查分类讨论的数学思想，正确分类是关键．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
3．f（x）是定义在[-3，3]上的奇函数，且x＞0时，f′（x）cosx＜f（x）sinx则不等式f（x）cosx＞0的解集是（ ）
| A． | [-3，0] | B． | $（-\frac{π}{2}，0）∪（\frac{π}{2}，3]$ | C． | $[-3，-\frac{π}{2}）∪（\frac{π}{2}，3]$ | D． | $[-3，-\frac{π}{2}）∪（0，\frac{π}{2}）$ |
1．
我校高二期中考试统一测试文科的数学成绩分组统计如下表：
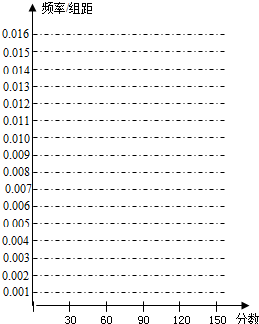
（Ⅰ）求出表中m、n、M、N的值，并根据表中所给数据在下面给出的坐标系中画出频率分布直方图；
（Ⅱ）若我校参加本次考试的文科学生有600人，试估计这次测试中我校成绩在90分以上的人数；
（Ⅲ）若我校教师拟从分数不超过60分的学生中选取2人进行个案分析，求被选中2人分数不超过30分的概率．
我校高二期中考试统一测试文科的数学成绩分组统计如下表：（Ⅰ）求出表中m、n、M、N的值，并根据表中所给数据在下面给出的坐标系中画出频率分布直方图；
| 分组 | 频数 | 频率 |
| （0，30] | 3 | 0.03 |
| （30，60] | 3 | 0.03 |
| （60，90] | 37 | 0.37 |
| （90，120] | m | n |
| （120，150] | 15 | 0.15 |
| 合计 | M | N |
（Ⅲ）若我校教师拟从分数不超过60分的学生中选取2人进行个案分析，求被选中2人分数不超过30分的概率．
5．已知A${\;}_{n}^{2}$=7A${\;}_{n-4}^{2}$，则n的值为（ ）
| A． | 7 | B． | 8 | C． | 9 | D． | 10 |