题目内容
3.若函数f(x)的自变量x在区间I上,恒有f(x)<0(或f(x)>0),则称f(x)是区间I上的“负任性函数”(或“正任性函数”).已知g(x)=x-$\frac{1}{x}$,函数f(x)=mg(x)+g(mx)是区间[1,+∞)上的“负任性函数”,则实数m的取值范围是(-∞,-1).分析 通过化简可知当x∈[1,+∞)f(x)=2mx-$\frac{{m}^{2}+1}{mx}$<0,当m>0时即解不等式2m2x2<m2+1,当m>0时即解不等式2m2x2>m2+1,计算即得结论.
解答 解:∵g(x)=x-$\frac{1}{x}$,
∴f(x)=mg(x)+g(mx)
=m(x-$\frac{1}{x}$)+mx-$\frac{1}{mx}$
=2mx-$\frac{{m}^{2}+1}{mx}$,
∵函数f(x)是区间[1,+∞)上的“负任性函数”,
∴当x∈[1,+∞),f(x)=2mx-$\frac{{m}^{2}+1}{mx}$<0,
下面对m的正负进行讨论:
①当m>0时,2mx-$\frac{{m}^{2}+1}{mx}$<0,即2m2x2<m2+1,
∴${m}^{2}<\frac{1}{2{x}^{2}-1}$,
∵x∈[1,+∞),
∴2x2-1∈[1,+∞),$\frac{1}{2{x}^{2}-1}$∈(0,1],
∴m2<0,无解;
②当m>0时,2mx-$\frac{{m}^{2}+1}{mx}$<0,即2m2x2>m2+1,
∴m2>$\frac{1}{2{x}^{2}-1}$,
∵x∈[1,+∞),
∴2x2-1∈[1,+∞),$\frac{1}{2{x}^{2}-1}$∈(0,1],
∴m2>1,
∴m<-1或m>1(舍);
综上所述:m<-1,
故答案为:(-∞,-1).
点评 本题考查函数的最值,涉及解不等式等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
13. 某人设计了一个图案如图所示,他有四个颜色想都涂在这个图案的六个区域中,相邻不能同色(如①②为相邻,①⑤为不相邻等),他有( )种涂色方法.
某人设计了一个图案如图所示,他有四个颜色想都涂在这个图案的六个区域中,相邻不能同色(如①②为相邻,①⑤为不相邻等),他有( )种涂色方法.
 某人设计了一个图案如图所示,他有四个颜色想都涂在这个图案的六个区域中,相邻不能同色(如①②为相邻,①⑤为不相邻等),他有( )种涂色方法.
某人设计了一个图案如图所示,他有四个颜色想都涂在这个图案的六个区域中,相邻不能同色(如①②为相邻,①⑤为不相邻等),他有( )种涂色方法.| A. | 408 | B. | 336 | C. | 360 | D. | 384 |
11. 某市热线网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票.按照该市暴雨前后两个时间收集了50份有效票,所得统计结果如下表:
某市热线网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票.按照该市暴雨前后两个时间收集了50份有效票,所得统计结果如下表:
已知工作人员从所有投票中任取一个,取到“不支持投入”的投票的概率为$\frac{2}{5}$.
(1)求列联表中的数据x,y,A,B的值;
(2)绘制条形统计图,通过图形判断本次暴雨是否影响到民众对加大修建城市地下排水设施的投入的态度?
(3)能够有多大把握认为暴雨与该市民众是否赞成加修建城市地下排水设施的投入有关?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$
 某市热线网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票.按照该市暴雨前后两个时间收集了50份有效票,所得统计结果如下表:
某市热线网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票.按照该市暴雨前后两个时间收集了50份有效票,所得统计结果如下表:| 支持 | 不支持 | 总计 | |
| 暴雨后 | x | y | 50 |
| 暴雨前 | 20 | 30 | 50 |
| 总计 | A | B | 100 |
(1)求列联表中的数据x,y,A,B的值;
(2)绘制条形统计图,通过图形判断本次暴雨是否影响到民众对加大修建城市地下排水设施的投入的态度?
(3)能够有多大把握认为暴雨与该市民众是否赞成加修建城市地下排水设施的投入有关?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$
| P(K2≤K0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.不等式x(x-1)≥x的解集为( )
| A. | {x|x≤0或x≥2} | B. | {x|0≤x≤3} | C. | {x|x≥2} | D. | {x|x≤0或x≥1} |
15.在△ABC中,(sinA+sinB)(sinA-sinB)≤sinC(sinC-sinB),则A的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6},π$) | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3},π$) |
13.计算22+42+62+…+1002的算法的程序框图是( )
| A. | 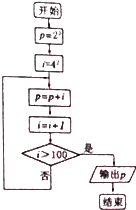 | B. | 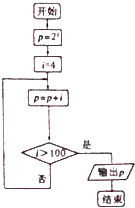 | C. | 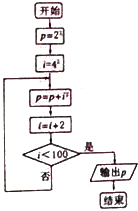 | D. | 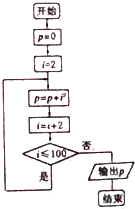 |