题目内容
【题目】如图，已知椭圆
（
）的离心率为
，以该椭圆上的点和椭圆的左、右焦点
，
为顶点的三角形的周长为
，一等轴双曲线的顶点是该椭圆的焦点，设
为该双曲线上异于顶点的任一点，直线
和
与椭圆的交点分别为
、
和
、
．
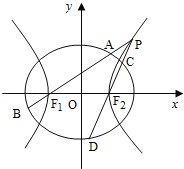
（1）求椭圆和双曲线的标准方程；
（2）设直线、的斜率分别为
、
，证明
为定值；
（3）是否存在常数
，使得
恒成立？若存在，求的值；若不存在，请说明理由．
【答案】（1）
；（2）见解析；（3）见解析
【解析】
（1）由题意知，椭圆离心率为
=
，及椭圆的定义得到又2a+2c=
，解方程组即可求得椭圆的方程，等轴双曲线的顶点是该椭圆的焦点可求得该双曲线的方程；
（2）设点P（x0，y0），根据斜率公式求得k1、k2，把点P（x0，y0）在双曲线上，即可证明结果；
（3）设直线AB的方程为y=k（x+2），则可求出直线CD的方程为y=
（x﹣2），联立直线和椭圆方程，利用韦达定理，即可求得|AB|，|CD|，代入|AB|+|CD|=λ|AB||CD|，求得λ的值．
（1）由题意知，椭圆离心率为=，
得
，又2a+2c=，
所以可解得
，c=2，所以b2=a2﹣c2=4，
所以椭圆的标准方程为
；
所以椭圆的焦点坐标为（±2，0），
因为双曲线为等轴双曲线，且顶点是该椭圆的焦点，
所以该双曲线的标准方程为
．
（2）设点P（x0，y0），
则k1=
，k2=
，
∴k1k2=
=
，
又点P（x0，y0）在双曲线上，
∴
，即y02=x02﹣4，
∴k1k2==1．
（3）假设存在常数λ，使得得|AB|+|CD|=λ|AB||CD|恒成立，
则由（2）知k1k2=1，
∴设直线AB的方程为y=k（x+2），则直线CD的方程为y=
（x﹣2），
由方程组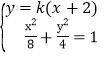
消y得：（2k2+1）x2+8k2x+8k2﹣8=0，
设A（x1，y1），B（x2，y2），
则由韦达定理得，
，
∴AB=
=
，
同理可得CD=
=
=
，
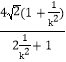∵|AB|+|CD|=λ|AB||CD|，
∴λ=
=﹣=
=
，
∴存在常数λ=，使得|AB|+|CD|=λ|AB||CD|恒成立．
