题目内容
【题目】世界读书日又称“世界图书日”,设立的目的是希望世界各地的人,无论你是年老还是年轻,都能享受阅读的乐趣,都能尊重和感谢为人类文明做出巨大贡献的文学、文化、科学、思想大师们,都能保护知识产权.某单位共有600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 150 | 210 | 180 | 60 |
约定:年龄在![]() 为青年人,在
为青年人,在![]() 为中老年人.今年年初,该单位开展“每天阅读1小时”活动,为了了解员工阅读1小时是否与年龄相关,一个月后按照分层抽样抽取30人进行调查.
为中老年人.今年年初,该单位开展“每天阅读1小时”活动,为了了解员工阅读1小时是否与年龄相关,一个月后按照分层抽样抽取30人进行调查.
(1)抽出的青年人与中老年人数量分别为多少?并估算单位这600人的平均年龄;
(2)若所抽取出的青年人与中老年人中分别有6人和7人平均每天阅读达1小时,其余人都没达1小时.完成下列2×2列联表,并回答能否由90%的把握认为年龄与阅读达1小时有关?
阅读达1小时 | 阅读没达1小时 | 总计 | |
青年 | 6 | ||
中年 | 7 | ||
总计 | 30 |
参考公式: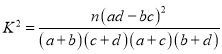
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】(1)18,12,42.5;(2)列联表见解析,没有90%的把握认为年龄与阅读达1小时有关.
【解析】
(1)由已知求得青年人与中老年人数量之比,然后按比例求出抽取的人数.根据人数分布表中数据中间点作为这组数据的估计值计算总均值.
(2)由(1)可得列联表中缺少的数据,然后根据公式计算![]() 可得.
可得.
(1)由题意,单位青年人与中老年人数量之比为![]() ,则由分层抽样可得,
,则由分层抽样可得,
抽出的青年人数量为![]() 人,中老年人数量为
人,中老年人数量为![]() 人;
人;
这600人的平均年龄为![]() .
.
(2)2×2列联表如下:
阅读达1小时 | 阅读没达1小时 | 总计 | |
青年 | 6 | 12 | 18 |
中年 | 7 | 5 | 12 |
总计 | 13 | 17 | 30 |
计算观测值![]()
∴没有90%的把握认为年龄与阅读达1小时有关.

【题目】“微信运动”已成为当下热门的健身方式,小明的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
| 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 |
|
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)若采用样本估计总体的方式,试估计小明的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步时被系统评定为“积极型”,否则为“懈怠型”.根据小明的统计完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 以上的把握认为“评定类型”与“性别”有关?
以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]()
![]()
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】为了研究一种昆虫的产卵数![]() 和温度
和温度![]() 是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
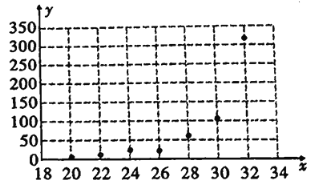
温度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数 | 6 | 10 | 22 | 26 | 64 | 118 | 310 |
|
|
|
|
|
|
|
26 | 79.4 | 3.58 | 112 | 11.6 | 2340 | 35.72 |
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该昆虫的产卵数
哪一个更适宜作为该昆虫的产卵数![]() 与温度
与温度![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据表中数据,建立![]() 关于
关于![]() 的回归方程;(保留两位有效数字)
的回归方程;(保留两位有效数字)
(3)根据![]() 关于
关于![]() 的回归方程,估计温度为33℃时的产卵数.
的回归方程,估计温度为33℃时的产卵数.
(参考数据:![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为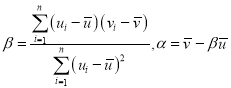 .
.