题目内容
非零向量
与
不共线，若
+
=
，
-
=
，则
⊥
是|
|=|
|的（ ）
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| d |
| c |
| d |
| a |
| b |
分析：利用充分条件和必要条件的定义，结合向量的数量积的应用进行判断．
解答：解：∵
+
=
，
-
=
，
∴若
⊥
，则
•
=(
+
)•(
-
)=0，
即
-
2=0，∴|
|=|
|成立．
若|
|=|
|，则
•
=(
+
)•(
-
)=
2-
2=|
|2-|
|2=0，
∴
⊥
，
∴
⊥
是|
|=|
|的充分且必要条件．
故选：C．
| a |
| b |
| c |
| a |
| b |
| d |
∴若
| c |
| d |
| c |
| d |
| a |
| b |
| a |
| b |
即
| a2 |
| b |
| a |
| b |
若|
| a |
| b |
| c |
| d |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴
| c |
| d |
∴
| c |
| d |
| a |
| b |
故选：C．
点评：本题主要考查充分条件和必要条件的应用，利用向量的数量积的应用是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
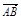=a+b,
=2a+8b,
=3(a-b)，求证：A、B、D三点共线；
=a+b,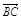
=2a+8b,
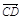=3(a-b)，求证：A、B、D三点共线；