题目内容
设两个非零向量| a |
| b |
(1)若
| AB |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
(2)试确定实数k,使k
| a |
| b |
| a |
| b |
分析:(1)根据所给的三个首尾相连的向量,用其中两个相加,得到两个首尾相连的向量,根据表示这两个向量的基底,得到两个向量之间的共线关系,从而得到三点共线.
(2)两个向量共线,写出向量共线的充要条件,进而得到关于实数k的等式,解出k的值,有两个结果,这两个结果都合题意.
(2)两个向量共线,写出向量共线的充要条件,进而得到关于实数k的等式,解出k的值,有两个结果,这两个结果都合题意.
解答:解:(1)∵
=
+
=2
+8
+3(
-
)
=5
+5
=5
,
∴
与
共线
两个向量有公共点B,
∴A,B,D三点共线.
(2)∵k
+
和
+k
共线,则存在实数λ,使得k
+
=λ(
+k
),
即(k-λ)
+(1-λk)
=
,
∵非零向量
与
不共线,
∴k-λ=0且1-λk=0,
∴k=±1.
| BD |
| BC |
| CD |
| a |
| b |
| a |
| b |
=5
| a |
| b |
| AB |
∴
| BD |
| AB |
两个向量有公共点B,
∴A,B,D三点共线.
(2)∵k
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
即(k-λ)
| a |
| b |
| 0 |
∵非零向量
| a |
| b |
∴k-λ=0且1-λk=0,
∴k=±1.
点评:本题考查向量共线定理,是一个基础题,本题从两个方面解读向量的共线定理,一是证明向量共线,一是根据两个向量共线解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
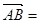 a
a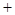 b,
b,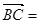 2a
2a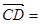 3(a- b)。求证:A、B、D三点共线;
3(a- b)。求证:A、B、D三点共线;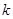 ,使
,使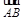 =a+b ,
=a+b ,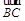 =2a+8b ,
=2a+8b ,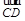 =3(a-b) ,
=3(a-b) ,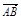 =a+b,
=a+b,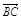 =2a+8b,
=2a+8b,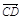 =3(a-b),求证:A、B、D三点共线;
=3(a-b),求证:A、B、D三点共线;