题目内容
(本题13分)
设两个非零向量a与b不共线,
(1)若向量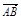 =a+b,
=a+b,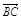 =2a+8b,
=2a+8b,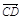 =3(a-b),求证:A、B、D三点共线;
=3(a-b),求证:A、B、D三点共线;
(2)试确定实数k,使向量ka+b和向量a+kb共线.
(1)略
(2)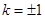
【解析】(1)证明 ∵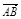 =a+b,
=a+b,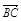 =2a+8b,
=2a+8b,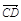 =3(a-b),
=3(a-b),
∴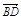 =
=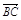 +
+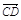 =2a+8b+3(a-b)=2a+8b+3a-3b=5(a+b) ………………2分
=2a+8b+3(a-b)=2a+8b+3a-3b=5(a+b) ………………2分
=5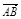 ………………4分
………………4分
∴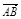 、
、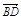 共线,
………………5分
共线,
………………5分
又∵它们有公共点B,∴A、B、D三点共线. ………………6分
(2)解 ∵ka+b与a+kb共线,
∴存在实数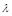 ,使ka+b=
,使ka+b=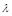 (a+kb),
……………8分
(a+kb),
……………8分
即ka+b=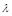 a+
a+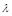 kb.
kb.
∴(k-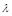 )a=(
)a=(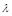 k-1)b ………………10分
k-1)b ………………10分
∵a、b是不共线的两个非零向量,
∴k-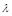 =
=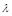 k-1=0,∴k2-1=0
………………12分
k-1=0,∴k2-1=0
………………12分
∴k=±1 ………………13分

(本题13分)最近北方遭受雪灾,蔬菜告急,南方某蔬菜公司要将一批蔬菜从南方A地运到北方B地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
| 运输工具 | 途中速度 (km/h) | 途中费用 (元/km) | 装卸时间 (h) | 装卸费用 (元) |
| 汽车 | 50 | 8 | 2 | 1000 |
| 火车 | 100 | 4 | 4 | 2000 |
若这批蔬菜在运输过程(含装卸时间)中损耗为300元/h,设A、B 两地距离为![]() km
km
(I)设采用汽车与火车运输的总费用分别为![]() 、
、![]() ,求
,求![]() 、
、![]() 的表达式;
的表达式;
(II)试根据A、B两地距离大小比较采用哪种运输工具比较好(即运输总费用最小).
(注:总费用=途中费用+装卸费用+损耗费用)
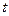 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为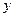 ,写出
,写出
 ,且
,且 ,
, ,求证:(1)
,求证:(1) 且
且 ;
; 在区间
在区间 内至少有一个零点;
内至少有一个零点; 是函数
是函数 .
.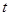 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为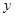 ,写出
,写出