题目内容
已知a>b>0,全集U=R,集合M={x|b<x<
},N={x|
<x<a},P={x|b<x≤
},则P,M,N满足的关系是( )
| a+b |
| 2 |
| ab |
| ab |
| A.P=M∪N | B.P=M∩N | C.P=M∩(CUN) | D.P=(CUM)∩N |
∵a>b>0,∴b<
<
<a.
∵N={x|
<x<a},全集U=R,画出数轴可知,∴CUN={x|x≤
,x≥a},
又M={x|b<x<
},
∴M∩(CUN)={x|b<x≤
},
又∵P={x|b<x≤
},∴M∩(CUN)=P.
故选C.
| ab |
| a+b |
| 2 |
∵N={x|
| ab |
| ab |
又M={x|b<x<
| a+b |
| 2 |
∴M∩(CUN)={x|b<x≤
| ab |
又∵P={x|b<x≤
| ab |
故选C.

练习册系列答案
相关题目
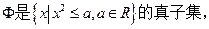 则实数a的取值范围是( )
则实数a的取值范围是( )
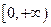
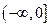
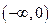
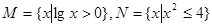 ,则
,则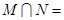 ( )
( )

