题目内容
如图,三棱锥P-ABC的三个侧面均为边长是1的等边三角形,M,N分别为PA,BC的中点.(1)求MN的长;
(2)求证:PA⊥BC;
(3)求三棱锥P-ABC的表面积.

【答案】分析:(1)先连接MB,MC.根据三棱锥P-ABC 的三个侧面均为边长是1 的等边三角形,得出底面△ABC 也是边长为1 的等边三角形.在Rt△MNB 中利用勾股定理即可求得MN的长;
(2)由M 是PA 的中点,得出 PA⊥MB,同理 PA⊥MC.根据线面垂直的判定定理得出 PA⊥平面MBC,再由线面垂直的性质定理可得 PA⊥BC;
(3)根据三棱锥P-ABC 的三个侧面和底面均为边长是1 的等边三角形,结合面积公式得出三棱锥P-ABC 的表面积.
解答: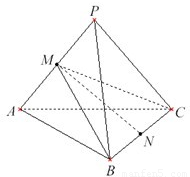 解:(1)连接MB,MC.
解:(1)连接MB,MC.
因为 三棱锥P-ABC 的三个侧面均为边长是1 的等边三角形,
所以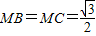 ,且底面△ABC 也是边长为1 的等边三角形.
,且底面△ABC 也是边长为1 的等边三角形.
因为 N 为BC 的中点,所以 MN⊥BC.在Rt△MNB 中,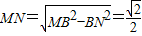 .…4分
.…4分
(2)证明:因为M 是PA 的中点,所以 PA⊥MB,同理 PA⊥MC.
因为 MB∩MC=M,所以 PA⊥平面MBC,
又因为 BC?平面MBC,所以 PA⊥BC.…8分
(3)因为 侧面等边三角形APB 的面积为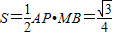 ,
,
且三棱锥P-ABC 的三个侧面和底面均为边长是1 的等边三角形,
所以 三棱锥P-ABC 的表面积为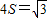 .…12分
.…12分
点评:本小题主要考查空间中直线与直线之间的位置关系、棱柱、棱锥、棱台的侧面积和表面积等基础知识,考查运算求解能力与转化思想.属于基础题.
(2)由M 是PA 的中点,得出 PA⊥MB,同理 PA⊥MC.根据线面垂直的判定定理得出 PA⊥平面MBC,再由线面垂直的性质定理可得 PA⊥BC;
(3)根据三棱锥P-ABC 的三个侧面和底面均为边长是1 的等边三角形,结合面积公式得出三棱锥P-ABC 的表面积.
解答:
 解:(1)连接MB,MC.
解:(1)连接MB,MC.因为 三棱锥P-ABC 的三个侧面均为边长是1 的等边三角形,
所以
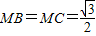 ,且底面△ABC 也是边长为1 的等边三角形.
,且底面△ABC 也是边长为1 的等边三角形.因为 N 为BC 的中点,所以 MN⊥BC.在Rt△MNB 中,
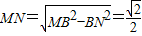 .…4分
.…4分(2)证明:因为M 是PA 的中点,所以 PA⊥MB,同理 PA⊥MC.
因为 MB∩MC=M,所以 PA⊥平面MBC,
又因为 BC?平面MBC,所以 PA⊥BC.…8分
(3)因为 侧面等边三角形APB 的面积为
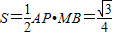 ,
,且三棱锥P-ABC 的三个侧面和底面均为边长是1 的等边三角形,
所以 三棱锥P-ABC 的表面积为
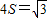 .…12分
.…12分点评:本小题主要考查空间中直线与直线之间的位置关系、棱柱、棱锥、棱台的侧面积和表面积等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中, (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,