题目内容
12.数列{an}的通项an=sin$\frac{nπ}{3}$,前n项和为Sn,则S2015等于( )| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
分析 通过an=sin$\frac{nπ}{3}$计算出数列的前几项可知数列{an}是周期为6的周期数列,且前6项的和为0,进而计算可得结论.
解答 解:∵an=sin$\frac{nπ}{3}$,
∴a1=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,a2=$sin\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,a3=sin$\frac{3π}{3}$=0,
a4=sin$\frac{4π}{3}$=-$\frac{\sqrt{3}}{2}$,a5=sin$\frac{5π}{3}$=-$\frac{\sqrt{3}}{2}$,a6=$sin\frac{6π}{3}$=0,
∴数列{an}是周期为6的周期数列,且前6项的和为0,
∵2015=6×335+5,
∴S2015=S5=0,
故选:B.
点评 本题考查数列的通项及前n项和,找出周期是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
 如图所示,在正方体ABCD-A1B1C1D1中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和平面ABC1D1均成30°角,则这样的直线l有( )
如图所示,在正方体ABCD-A1B1C1D1中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和平面ABC1D1均成30°角,则这样的直线l有( )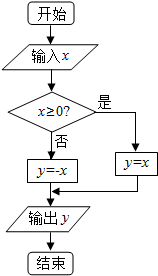 阅读如图所示的程序框图.
阅读如图所示的程序框图. 如图,某市若规划一居民小区ABCD,AD=2千米,AB=1千米,∠A=90°,政府决定从该地块中划出一个直角三角形地块AEF建活动休闲区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为1千米,△AEF的面积为S.
如图,某市若规划一居民小区ABCD,AD=2千米,AB=1千米,∠A=90°,政府决定从该地块中划出一个直角三角形地块AEF建活动休闲区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为1千米,△AEF的面积为S.