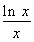Question

设f(x)是(-∞,+∞)上的奇函数,且f(x+2)=-f(x),下面关于f(x)的判定:其中正确命题的序号为　　　　.

①f(4)=0;

②f(x)是以4为周期的函数;

③f(x)的图象关于x=1对称;

④f(x)的图象关于x=2对称.

 

Answer 1

①②③

【解析】∵f(x+2)=-f(x),

∴f(x)=-f(x+2)=-(-f(x+2+2))=f(x+4),

即f(x)的周期为4,②正确.

∴f(4)=f(0)=0(∵f(x)为奇函数),即①正确.

又∵f(x+2)=-f(x)=f(-x),

∴f(x)的图象关于x=1对称,∴③正确.

又∵f(1)=-f(3),当f(1)≠0时,显然f(x)的图象不关于x=2对称,∴④错误.