Question

【题目】已知正方体的棱长为，其内有2个不同的小球，球与三棱锥的四个面都相切，球与三棱锥的三个面和球都相切，则球的体积等于______，球的表面积等于______．

Answer 1

【答案】

【解析】

由题意可知三棱锥是边长为的正四面体,则球是三棱锥的内切球,设其半径为,由，可知,设平面平面,且球和球均与平面相切于点,则球是正四面体的内切球,设其半径为,则,最后代入数据计算即可.

因为正方体的棱长为,

所以三棱锥是边长为的正四面体,的高为,

设底面的中心为,连接,则,,

则球是三棱锥的内切球,设其半径为,

则有

所以,

所以球的体积为,

又球与三棱锥的三个面和球都相切,

则设平面平面,且球和球均与平面相切于点,如下图所示,

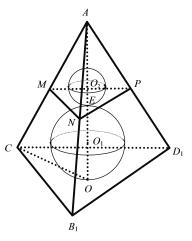
则球是三棱锥的内切球,设其半径为,

故,

因此在正四面体中,,

所以球的表面积为,

故答案为:;.