题目内容
【题目】新型冠状病毒肺炎是一种急性感染性肺炎，其病原体是一种先前未在人类中发现的新型冠状病毒，即2019新型冠状病毒.2020年2月7日，国家卫健委决定将“新型冠状病毒感染的肺炎”暂命名为“新型冠状病毒肺炎”，简称“新冠肺炎”.患者初始症状多为发热、乏力和干咳，并逐渐出现呼吸困难等严重表现.基于目前流行病学调查，潜伏期为1~14天，潜伏期具有传染性，无症状感染者也可能成为传染源.某市为了增强民众防控病毒的意识，举行了“预防新冠病毒知识竞赛”网上答题，随机抽取
人，答题成绩统计如图所示.
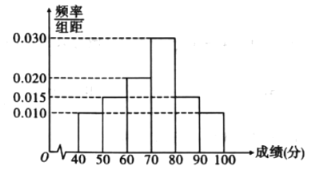
（1）由直方图可认为答题者的成绩
服从正态分布
，其中
分别为答题者的平均成绩
和成绩的方差
，那么这名答题者成绩超过
分的人数估计有多少人？（同一组中的数据用该组的区间中点值作代表）
（2）如果成绩超过
分的民众我们认为是“防御知识合格者”，用这名答题者的成绩来估计全市的民众，现从全市中随机抽取
人，“防御知识合格者”的人数为
，求
.（精确到
）
附：①
，
；②
，则
，
；③
，
.
【答案】（1）
人（2）
【解析】
（1）由频率分布直方图求得
，
服从正态分布
根据提供的数据，得到
，然后通过
法则求解.
（2）由（1）知，成绩超过
的概率为
，
，利用二项分布公式求解.
（1）由题意知：
.
因为服从正态分布，其中
，
，
，
∴服从正态分布，
而
，
∴
，
∴竞赛成绩超过
的人数估计为
人.
（2）由（1）知，成绩超过的概率为，
而，
∴
.
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
