题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的中心为坐标原点
的中心为坐标原点![]() 焦点在
焦点在![]() 轴上,右顶点
轴上,右顶点![]() 到右焦点的距离与它到右准线的距离之比为
到右焦点的距离与它到右准线的距离之比为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两点,设
轴对称的任意两点,设![]() ,连接
,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .求证:直线
.求证:直线![]() 过定点
过定点![]() 并求出点
并求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)证明详见解析,
;(2)证明详见解析,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意列出关于![]() 的等式求解即可.
的等式求解即可.
(2)先根据对称性,直线![]() 过的定点
过的定点![]() 一定在
一定在![]() 轴上,再设直线
轴上,再设直线![]() 的方程为
的方程为![]() ,联立直线与椭圆的方程, 进而求得
,联立直线与椭圆的方程, 进而求得![]() 的方程,并代入
的方程,并代入![]() ,
,![]() 化简分析即可.
化简分析即可.
(3)先分析过点![]() 的直线
的直线![]() 斜率不存在时
斜率不存在时![]() 的值,再分析存在时,设直线
的值,再分析存在时,设直线![]() 的方程为
的方程为![]() ,联立直线与椭圆的方程,得出韦达定理再代入
,联立直线与椭圆的方程,得出韦达定理再代入![]() 求解出关于
求解出关于![]() 的解析式,再求解范围即可.
的解析式,再求解范围即可.
解:![]() 设椭圆
设椭圆![]() 的标准方程
的标准方程![]() 焦距为
焦距为![]() ,
,
由题意得,![]()
由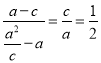 ,可得
,可得![]()
则![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() ;
;
![]() 证明:根据对称性,直线
证明:根据对称性,直线![]() 过的定点
过的定点![]() 一定在
一定在![]() 轴上,
轴上,
由题意可知直线![]() 的斜率存在,
的斜率存在,
设直线![]() 的方程为
的方程为![]() ,
,
联立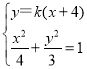 ,消去
,消去![]() 得到
得到![]() ,
,
设点![]() ,
,
则![]() .
.
所以![]() ,
,
所以![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() ,
,
将![]() ,
,![]() 代入上式并整理,
代入上式并整理,
![]() ,
,
整理得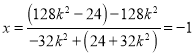 ,
,
所以,直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() .
.
![]() 当过点
当过点![]() 的直线
的直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]()
![]() ,
,
此时![]() ,
,
当过点![]() 的直线
的直线![]() 斜率存在时,
斜率存在时,
设直线![]() 的方程为
的方程为![]() ,且
,且![]() 在椭圆
在椭圆![]() 上,
上,
联立方程组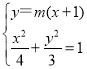 ,
,
消去![]() ,整理得
,整理得![]() ,
,
则![]() .
.
所以![]()
所以![]() ,
,
所以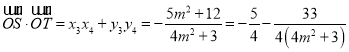 ,
,
由![]() 得
得![]() ,
,
综上可得,![]() 的取值范围是
的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】《周易》历来被人们视作儒家群经之首,它表现了古代中华民族对万事万物的深刻而又朴素的认识,是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法.我们用近代术语解释为:把阳爻“- ”当作数字“1”,把阴爻“--”当作数字“0”,则八卦所代表的数表示如下:
卦名 | 符号 | 表示的二进制数 | 表示的十进制数 |
坤 |
| 000 | 0 |
震 |
| 001 | 1 |
坎 |
| 010 | 2 |
兑 |
| 011 | 3 |
依此类推,则六十四卦中的“屯”卦,符号“![]() ”表示的十进制数是( )
”表示的十进制数是( )
A. 18B. 17C. 16D. 15