题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)判断并说明函数![]() 的零点个数.若函数
的零点个数.若函数![]() 所有零点均在区间
所有零点均在区间![]()
![]() 内,求
内,求![]() 的最小值.
的最小值.
【答案】(1)分类讨论,详见解析;(2)![]() 存在两个零点
存在两个零点![]() ,且
,且![]() ,
,![]() ;
;![]() 最小值为3.
最小值为3.
【解析】
(1)直接求导即可;
(2)![]() ,为判断出
,为判断出![]() 符号,分成3段处理:第一段
符号,分成3段处理:第一段![]() ,第二段
,第二段![]() ,第三段
,第三段![]() ,第四段
,第四段![]() 分别研究.
分别研究.
解:![]()
![]() 的定义域为
的定义域为![]()
![]()
令![]() 得
得![]()
![]() (舍).当
(舍).当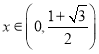 时,
时,![]() ,
,
当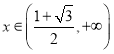 时,
时,![]() ,所以
,所以![]() 在
在 上单调递增,在
上单调递增,在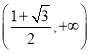 上单调递减,
上单调递减,
因此,函数![]() 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为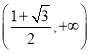
![]()
![]() ,
,
当![]() 时,
时,![]() ,所以,
,所以,![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
![]() ,所以存在唯一
,所以存在唯一![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,![]() 所以
所以![]()
单调递减,又![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上单调递
上单调递
增,因为![]() ,所以
,所以![]() ,故不存在零点;当
,故不存在零点;当![]() 时,
时,
![]() ,
,![]() ,所以
,所以![]() 单调递减,
单调递减,
又![]() ,
,![]() 所以存在
所以存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调
单调
递减,又![]() ,
,![]() ,
,
![]() ,所以存在唯一
,所以存在唯一![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,故不存在零点.
,故不存在零点.
综上,![]() 存在两个零点
存在两个零点![]() ,且
,且![]() ,
,![]()
因此![]() 的最小值为
的最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在创建“全国文明卫生城”过程中,运城市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次),通过随机抽样,得到参加问卷调查的![]() 人的得分统计结果如表所示:.
人的得分统计结果如表所示:.
组别 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)由频数分布表可以大致认为,此次问卷调查的得分![]() 似为这
似为这![]() 人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求
人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求![]() ;
;
(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() 的可以获赠
的可以获赠![]() 次随机话费,得分低于
次随机话费,得分低于![]() 的可以获赠
的可以获赠![]() 次随机话费;
次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元) |
|
|
概率 |
|
|
现有市民甲参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:参考数据与公式:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]()
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):若分数不低于95分,则称该员工的成绩为“优秀”.
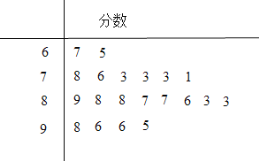

组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)从这20人中成绩为“优秀”的员工中任取2人,求恰有1人的分数为96的概率;
(Ⅱ)根据这20人的分数补全频率分布表和频率分布直方图,并根据频率分布直方图估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表).