题目内容
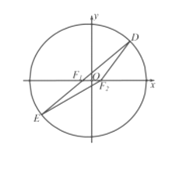
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 右顶点为
右顶点为![]() 过右焦点且垂直于
过右焦点且垂直于![]() 轴的直线与椭圆相交于
轴的直线与椭圆相交于![]() 两点,所得四边形
两点,所得四边形![]() 为菱形,且其面积为
为菱形,且其面积为![]() .
.
(1)求椭圆的方程;
(2)过左焦点![]() 的直线
的直线![]() 与椭圆交于
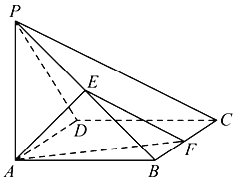
与椭圆交于![]() 两点,试求三角形
两点,试求三角形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由椭圆的对称性及四边形为![]() 菱形知
菱形知![]() ,可得
,可得![]() 的纵坐标为
的纵坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,结合
,结合![]() 的关系求解出
的关系求解出![]() ,即可得到得答案.
,即可得到得答案.
(2) 设![]() ,设直线
,设直线![]() 的方程为:
的方程为:![]() 由直线方程与椭圆方程联立,得到
由直线方程与椭圆方程联立,得到![]()
![]() 的表达式,求出三角形
的表达式,求出三角形![]() 面积的表达式,再求其最大值.
面积的表达式,再求其最大值.
(1)如图,因椭圆的对称性及四边形为![]() 菱形知
菱形知![]() ,
,
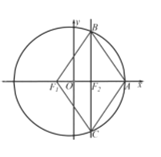
即![]() ,即
,即![]() ①
①
令![]() ,得点
,得点![]() 的纵坐标为
的纵坐标为![]()
由四边形![]() 的面积为
的面积为![]()
故![]()
即![]()
![]()
又![]() ③
③
联立![]() 得:
得: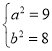
故椭圆方程为![]()
(2)由![]() 知:
知:![]()
设直线![]() 的方程为:
的方程为:![]()
假设![]() .
.
由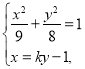 得:
得: ![]()
即![]()
由![]() 得:
得:
![]() ,故
,故![]() .
.
![]()
![]()
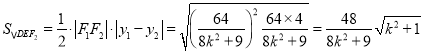
令![]()
则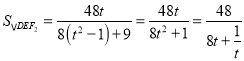
设![]()
由![]() 可知:
可知: ![]() 单调递增,
单调递增,
![]()
故![]()

 名校课堂系列答案
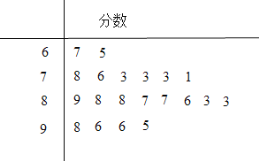
名校课堂系列答案【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):若分数不低于95分,则称该员工的成绩为“优秀”.

组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)从这20人中成绩为“优秀”的员工中任取2人,求恰有1人的分数为96的概率;
(Ⅱ)根据这20人的分数补全频率分布表和频率分布直方图,并根据频率分布直方图估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表).
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: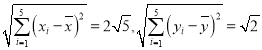
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: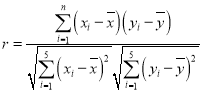 ,
,
参考数据:![]()