题目内容
双曲线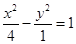 的渐近线方程是
的渐近线方程是
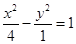 的渐近线方程是
的渐近线方程是 A.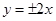 | B.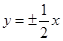 | C.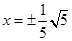 | D.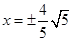 |
B
专题:计算题.
分析:渐近线方程是
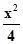 -y2=0,整理后就得到双曲线的渐近线.
-y2=0,整理后就得到双曲线的渐近线.解答:解:双曲线
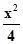 -y2=1
-y2=1其渐近线方程是
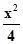 -y2=0
-y2=0整理得 x±2y=0.
故选B.
点评:本题考查了双曲线的渐进方程,把双曲线的标准方程中的“1”转化成“0”即可求出渐进方程.属于基础题.

练习册系列答案
相关题目
题目内容
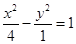 的渐近线方程是
的渐近线方程是 A.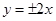 | B.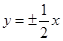 | C.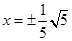 | D.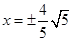 |
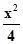 -y2=0,整理后就得到双曲线的渐近线.
-y2=0,整理后就得到双曲线的渐近线.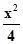 -y2=1
-y2=1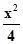 -y2=0
-y2=0