题目内容
【题目】已知函数![]() .
.
(Ⅰ)求函数f(x)的定义域,判断并证明函数f(x)的奇偶性;
(Ⅱ)是否存在这样的实数k,使f(k-x2)+f(2k-x4)≥0对一切![]() 恒成立,若存在,试求出k的取值集合;若不存在,请说明理由.
恒成立,若存在,试求出k的取值集合;若不存在,请说明理由.
【答案】(Ⅰ)见解析; (Ⅱ)不存在满足题意的实数k.
【解析】
(Ⅰ)真数大于0解不等式可得定义域;奇偶性定义判断奇偶性;
(Ⅱ)假设存在实数k后,利用奇偶性和单调性去掉函数符号后变成具体不等数组,然后转化为最值即可得.
(Ⅰ)由![]() >0 得-2<x<2,
>0 得-2<x<2,
所以f(x)的定义域为(-2,2);
∵f(-x)=lg![]() =-lg
=-lg![]() =-f(x),
=-f(x),
∴f(x)是奇函数.
(Ⅱ)假设存在满足题意的实数k,则
令t=![]() =
=![]() =
=![]() -1,x∈(-2,2),
-1,x∈(-2,2),
则t在(-2,2)上单调递减,又y=lgt在(0,+∞)上单调递增,
于是函数f(x)在(-2,2)上单调递减,
∴已知不等式f(k-x2)+f(2k-x4)≥0f(k-x2)≥-f(2k-x4)
f(k-x2)≥f(x4-2k)-2<k-x2≤x4-2k<2,
由题意知-2<k-x2≤x4-2k<2对一切x∈[-![]() ,
,![]() ]恒成立,
]恒成立,
得不等式组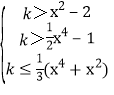 对一切x∈[-
对一切x∈[-![]() ,
,![]() ]恒成立,
]恒成立,
∴ ,即k∈.
,即k∈.
故不存在满足题意的实数k.

 阅读快车系列答案
阅读快车系列答案【题目】已知△ABC的边AB所在直线方程为y=3x,BC所在直线方程为y=ax+12,AC边上的高BD所在直线方程为y=﹣x+8.
(1)求实数a的值;
(2)若AC边上的高BD![]() ,求边AC所在的直线方程.
,求边AC所在的直线方程.
【题目】某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中,能较好地反映计算机在第![]() 天被感染的数量
天被感染的数量![]() 与
与![]() 之间的关系的是
之间的关系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【题目】某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率有帮助”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
60分及以下 | 61~70分 | 71~80分 | 81~90分 | 91~100分 | |
甲班(人数) | 3 | 6 | 12 | 15 | 9 |
乙班(人数) | 4 | 7 | 16 | 12 | 6 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)由以上统计数据填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
(2)对甲乙两班60分及以下的同学进行定期辅导,一个月后从中抽取3人课堂检测,![]() 表示抽取到的甲班学生人数,求
表示抽取到的甲班学生人数,求![]() 及至少抽到甲班1名同学的概率.
及至少抽到甲班1名同学的概率.
【题目】2018年4月4日召开的国务院常务会议明确将进一步推动网络提速降费工作落实,推动我国数字经济发展和信息消费,今年移动流量资费将再降![]() 以上,为响应国家政策,某通讯商计划推出两款优惠流量套餐,详情如下:
以上,为响应国家政策,某通讯商计划推出两款优惠流量套餐,详情如下:
套餐名称 | 月套餐费/元 | 月套餐流量/M |
A | 30 | 3000 |
B | 50 | 6000 |
这两款套餐均有以下附加条款:套餐费用月初一次性收取,手机使用流量一旦超出套餐流量,系统就会自动帮用户充值![]() 流量,资费20元;如果又超出充值流量,系统再次自动帮用户充值
流量,资费20元;如果又超出充值流量,系统再次自动帮用户充值![]() 流量,资费20元,以此类推.此外,若当月流量有剩余,系统将自动清零,不可次月使用.
流量,资费20元,以此类推.此外,若当月流量有剩余,系统将自动清零,不可次月使用.
小张过去50个月的手机月使用流量(单位:M)的频数分布表如下:
月使用流量分组 |
|
|
|
|
|
|
频数 | 4 | 5 | 11 | 16 | 12 | 2 |
根据小张过去50个月的手机月使用流量情况,回答以下几个问题:
(1)若小张选择A套餐,将以上频率作为概率,求小张在某一个月流量费用超过50元的概率;
(2)小张拟从A或B套餐中选定一款,若以月平均费用作为决策依据,他应订哪一种套餐?说明理由.
