题目内容
已知向量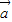
=（5，-3），
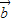=（9，-6-cosα），α是第二象限角，
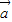∥（2
-
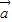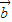），则tanα= ．
【答案】分析：由题意可得向量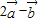
的坐标，进而由向量平行的条件可得cosα=
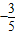，结合a是第二象限角可得sinα，由三角函数关系可得答案．
解答：解：由题意可得：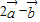
=2（5，-3）-（9，-6-cosα）=（1，cosα），
∵
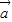∥（2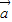
-
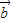），∴5cosα-（-3）×1=0，解得cosα=
，
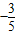又因为α是第二象限角，∴sinα=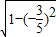
=
，
故tanα=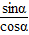
=
，
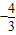故答案为：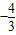
点评：本题为三角函数与向量的综合应用，涉及向量平行的充要条件，属基础题．
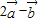的坐标，进而由向量平行的条件可得cosα=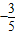，结合a是第二象限角可得sinα，由三角函数关系可得答案．解答：解：由题意可得：
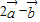=2（5，-3）-（9，-6-cosα）=（1，cosα），∵
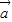∥（2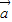-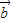），∴5cosα-（-3）×1=0，解得cosα=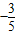，又因为α是第二象限角，∴sinα=
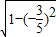=，故tanα=
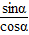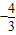=，故答案为：
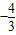
点评：本题为三角函数与向量的综合应用，涉及向量平行的充要条件，属基础题．
练习册系列答案
名题金卷系列答案
相关题目
已知向量
=(x-5，3)，
=(2，x)，且
⊥
，则由x的值构成的集合是（ ）
| a |
| b |
| a |
| b |
| A、{2，3} | B、{-1，6} |
| C、{2} | D、{6} |
已知向量
=（-5，3），
=（2，x），且
∥
，则x的值是（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|