题目内容
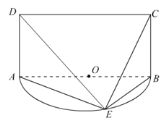
【题目】如图,E是以AB为直径的半圆O上异于A、B的点,矩形ABCD所在的平面垂直于半圆O所在的平面,且AB=2AD=2.
(1)求证:![]() ;
;
(2)若异面直线AE和DC所成的角为![]() ,求平面DCE与平面AEB所成的锐二面角的余弦值.
,求平面DCE与平面AEB所成的锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1) 由面面垂直的性质可证得![]() .再线面垂直的判定定理和性质定理可得证;
.再线面垂直的判定定理和性质定理可得证;
(2)以点![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,过点
轴,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .由二面角的向量求解方法可求得平面DCE与平面AEB所成的锐二面角的余弦值.
.由二面角的向量求解方法可求得平面DCE与平面AEB所成的锐二面角的余弦值.
(1) ∵平面![]() 垂直于圆
垂直于圆![]() 所在的平面,
所在的平面,
两平面的交线为![]() 平面
平面![]() ,
,
∴![]() 垂直于圆
垂直于圆![]() 所在的平面.又
所在的平面.又![]() 在圆
在圆![]() 所在的平面内,
所在的平面内,
∴![]() .∵
.∵![]() 是直角,∴
是直角,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() .
.
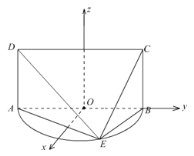
(2)如图, 以点![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,
过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
由异面直线![]() 和
和![]() 所成的角为
所成的角为![]() ,
,![]() ,
,
知![]() ,∴
,∴![]() ,
,
∴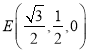 ,由题设可知
,由题设可知 ![]() ,
,![]() ,
,
∴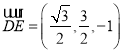 ,
,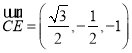 .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由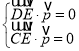 ,即
,即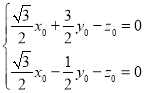
得![]() ,
,![]() ,取
,取![]() ,得
,得![]() .
.
∴![]() .又平面
.又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴ .
.
平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值
所成的锐二面角的余弦值![]() .
.

【题目】腾飞中学学生积极参加科技创新大赛,在市级组织的大赛中屡创佳绩.为了组织学生参加下一届市级大赛,了解学生报名参加社会科学类比赛(以下称为A类比赛)和自然科学类比赛(以下称为B类比赛)的意向,校团委随机调查了60名男生和40名女生调查结果如下:60名男生中,15名不准备参加比赛,5名准备参加A类比赛和B类比赛,剩余的男生有![]() 准备参加A类比赛,
准备参加A类比赛,![]() 准备参加B类比赛,40名女生中,10名不准备参加比赛,25名准备参加A类比赛,5名准备参加B类比赛.
准备参加B类比赛,40名女生中,10名不准备参加比赛,25名准备参加A类比赛,5名准备参加B类比赛.
(1)根据统计数据,完成如2×2列联表(A类比赛和B类比赛都参加的学生需重复统计):
A类比赛 | B类比赛 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)能否有99%的把握认为学生参加A类比赛或B类比赛与性别有关?
附:K2![]() .
.
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】新冠疫情发生后,酒精使用量大增,某生产企业调整设备,全力生产![]() 与
与![]() 两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量
两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量![]() (单位:吨)与时间n(
(单位:吨)与时间n(![]() 且
且![]() )成等差数列,且
)成等差数列,且![]() ,
,![]() .又知
.又知![]() 酒精日产量所占比重
酒精日产量所占比重![]() 与时间n成等比数列,
与时间n成等比数列,![]() 酒精日产量所占比重与时间n的关系如下表(
酒精日产量所占比重与时间n的关系如下表(![]() ):
):
|
|
|
| …… |
时间n | 1 | 2 | 3 | …… |
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() ,求前n天
,求前n天![]() (单位:吨,
(单位:吨,![]() 且
且![]() ).
).