题目内容
【题目】在四棱锥S—ABCD中,底面ABCD为长方形,SB⊥底面ABCD,其中BS=2,BA=2,BC=λ,λ的可能取值为:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤λ=3
;⑤λ=3

(1)求直线AS与平面ABCD所成角的正弦值;
(2)若线段CD上能找到点E,满足AE⊥SE,则λ可能的取值有几种情况?请说明理由;
(3)在(2)的条件下,当λ为所有可能情况的最大值时,线段CD上满足AE⊥SE的点有两个,分别记为E1,E2,求二面角E1-SB-E2的大小.
【答案】(1)![]() (2)λ可以取①②③,见解析(3)30°
(2)λ可以取①②③,见解析(3)30°
【解析】
(1)由![]() 底面
底面![]() ,得
,得![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,由此能求出直线
所成的角,由此能求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(2)以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 的方向分别为
的方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向建立空间直角坐标系,根据
轴正方向建立空间直角坐标系,根据![]() 得到
得到![]() ,再根据
,再根据![]() 的取值范围得到
的取值范围得到![]() 的取值;
的取值;
(3)利用向量法能求出![]() 夹角的余弦值,进而求得二面角
夹角的余弦值,进而求得二面角![]() 的大小.
的大小.
(1)因为SB⊥底面ABCD,所以∠SAB即为直线AS与平面ABCD所成的角,
在![]() 中,
中,![]()
(2)以B为坐标原点,以BC、BA、BS的方向分别为x轴、y轴z轴正方向建立如图所示的空间直角坐标系,则各点坐标分别为:
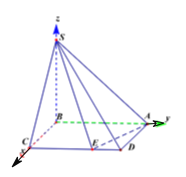
B(0,0,0),A(0,2,0),D(λ,2,0),S(0,0,2).
设![]() ,所以,
,所以,
![]()
![]()
因为x∈[0,2], ![]() ,所以在所给的数据中,λ可以取①②③
,所以在所给的数据中,λ可以取①②③
(3)由(2)知![]() ,此时,
,此时,![]() 或
或![]() ,即满足条件的点E有两个,
,即满足条件的点E有两个,
根据题意得,其坐标为![]() 和
和![]() ,
,
因为SB⊥平面ABCD,所以SB⊥BE1, SB⊥BE2,
所以,∠E1BE2是二面角E1SBE2的平面角
由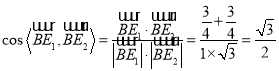
由题意得二面角E1SBE2为锐角,
所以二面角E1SBE2的大小为30°

 名校课堂系列答案
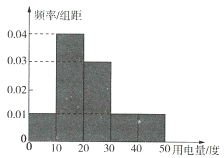
名校课堂系列答案【题目】随着互联网的不断发展,手机打车软件APP也不断推出.在某地有AB两款打车APP,为了调查这两款软件叫车后等候的时间,用这两款APP分别随机叫了50辆车,记录了候车时间如下表:
A款软件:
候车时间(分钟) |
|
|
|
|
|
|
车辆数 | 2 | 12 | 8 | 12 | 14 | 2 |
B款软件:
候车时间(分钟) |
|
|
|
|
|
|
车辆数 | 2 | 10 | 28 | 7 | 2 | 1 |
(1)试画出A款软件候车时间的频率分布直方图,并估计它的众数及中位数;
(2)根据题中所给的数据,将频率视为概率
(i)能否认为B款软件打车的候车时间不超过6分钟的概率达到了75%以上?
(ii)仅从两款软件的平均候车时间来看,你会选择哪款打车软件?