Question

（本小题满分16分）
已知圆C过点P(1，1)，且与圆M：＋＝(r＞0)关于直线x＋y＋2＝0对称．
（1）求圆C的方程；
（2）直线l过点Q(1，0.5),截圆C所得的弦长为2,求直线l的方程；
（3）过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．

Answer 1

（1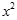）＋＝2（2）x=1;3x+4y-5=0（3）直线OP和AB平行．

解析试题分析：（1）设圆心C(a，b)，则解得
则圆C的方程为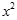＋＝，将点P坐标代入，得＝2，故圆C的方程为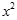＋＝2．
（2）直线l的方程为：x=1;3x+4y-5=0
（3）由题意，知直线PA和直线PB的斜率存在，且互为相反数，故可设
PA：y－1＝k(x－1)，PB：y－1＝－k(x－1)．
由得＋2k(1－k)x＋－2＝0．
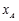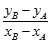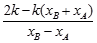因为点P的横坐标x＝1一定是该方程的解，故可得＝，同理＝．所以＝＝＝＝1＝．
所以直线OP和AB一定平行．
考点：圆的方程，直线和圆的位置关系
点评：在本题第2小题中注意考虑直线斜率不存在的情况