题目内容
函数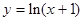
(1)若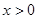 ,证明
,证明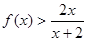 ;
;
(2)若不等式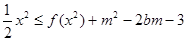 时
时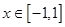 和
和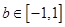 都恒成立,求实数
都恒成立,求实数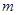 的取值范围。
的取值范围。
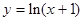
(1)若
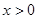 ,证明
,证明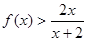 ;
;(2)若不等式
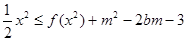 时
时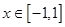 和
和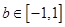 都恒成立,求实数
都恒成立,求实数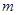 的取值范围。
的取值范围。(1)构造函数g(x)="f(x)-" 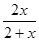 ,利用导数来判定单调性得到证明。
,利用导数来判定单调性得到证明。
(2)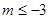 或
或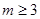
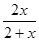 ,利用导数来判定单调性得到证明。
,利用导数来判定单调性得到证明。(2)
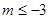 或
或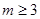
试题分析:(1)令g(x)="f(x)-"
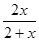 ="ln(x+1)-"
="ln(x+1)-" 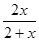 ,
,则g′(x)=
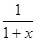 -
-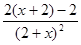 ∵x>0,
∵x>0,∴g′(x)>0,∴g(x)在(0,+∞)上是增函数.
故g(x)>g(0)=0,即f(x)>
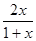
(2)原不等式等价于
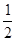 x2-f(x2)≤m2-2bm-3.
x2-f(x2)≤m2-2bm-3.令h(x)=
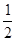 x2-f(x2)=
x2-f(x2)=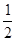 x2-ln(1+x2),
x2-ln(1+x2),则h′(x)=x-
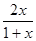 =
=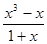
令h′(x)=0,得x=0,x=1,x=-1.
∴当x∈[-1,1]时,h(x)max=0,
∴m2-2bm-3≥0.令Q(b)=-2mb+m2-3,
则Q(1)=m2-2m-3≥0, Q(-1)=m2+2m-3≥0
解得m≤-3或m≥3.
点评:本题考查函数的导数和函数思想的应用,本题解题的关键是构造新函数,对于新函数进行求导求最值,再利用函数的思想来解题,这种题目可以出现在高考卷中

练习册系列答案
相关题目
 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 所成的小于
所成的小于 的角为
的角为 .
.
 关于
关于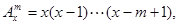 其中
其中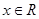 ,
,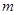 为正整数,且
为正整数,且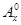 =1,这是排列数
=1,这是排列数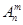 (
(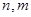 是正整数,
是正整数,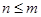 )的一种推广.
)的一种推广.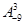 的值;
的值;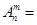
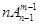 ,②
,②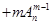
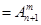 (其中m,n是正整数).是否都能推广到
(其中m,n是正整数).是否都能推广到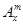 (
(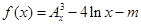 ,试讨论函数
,试讨论函数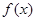 的零点个数.
的零点个数. ,有
,有 ,且
,且 时
时 ,则
,则 时( )
时( )


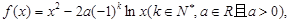
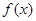 的单调性;
的单调性;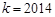 时,关于
时,关于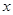 的方程
的方程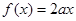 有唯一解,求
有唯一解,求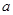 的值;
的值;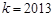 时,证明: 对一切
时,证明: 对一切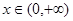 ,都有
,都有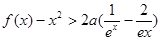 成立.
成立.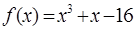 .
.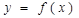 在点
在点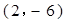 处的切线方程;
处的切线方程;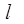 为曲线
为曲线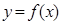 的切线,且经过原点,求直线
的切线,且经过原点,求直线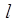 的方程及切点坐标
的方程及切点坐标 且
且 则
则 = ( )
= ( )



 _________________;
_________________; 在
在 上可导,且
上可导,且 ,
, __
__
