题目内容
规定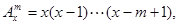 其中
其中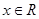 ,
,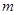 为正整数,且
为正整数,且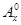 =1,这是排列数
=1,这是排列数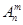 (
(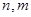 是正整数,
是正整数,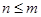 )的一种推广.
)的一种推广.
(Ⅰ) 求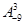 的值;
的值;
(Ⅱ)排列数的两个性质:①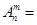
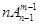 ,②
,②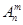
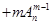
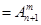 (其中m,n是正整数).是否都能推广到
(其中m,n是正整数).是否都能推广到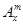 (
(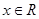 ,
,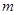 是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(Ⅲ)已知函数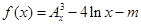 ,试讨论函数
,试讨论函数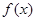 的零点个数.
的零点个数.
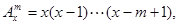 其中
其中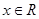 ,
,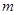 为正整数,且
为正整数,且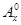 =1,这是排列数
=1,这是排列数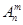 (
(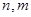 是正整数,
是正整数,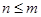 )的一种推广.
)的一种推广.(Ⅰ) 求
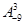 的值;
的值;(Ⅱ)排列数的两个性质:①
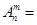
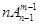 ,②
,②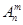
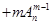
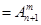 (其中m,n是正整数).是否都能推广到
(其中m,n是正整数).是否都能推广到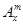 (
(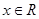 ,
,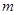 是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;(Ⅲ)已知函数
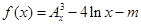 ,试讨论函数
,试讨论函数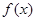 的零点个数.
的零点个数.(1)-990
(2)①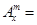
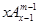 ,②
,②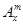
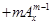
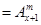 (
(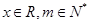 )
)
(3)当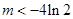 时,函数
时,函数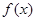 不存在零点,
不存在零点,
当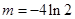 时,函数
时,函数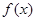 有且只有一个零点,
有且只有一个零点,
当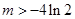 时,即函数
时,即函数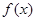 有且只有两个零点.
有且只有两个零点.
(2)①
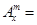
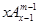 ,②
,②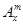
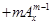
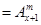 (
(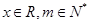 )
)(3)当
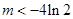 时,函数
时,函数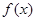 不存在零点,
不存在零点,当
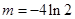 时,函数
时,函数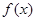 有且只有一个零点,
有且只有一个零点,当
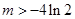 时,即函数
时,即函数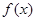 有且只有两个零点.
有且只有两个零点.试题分析:解:(Ⅰ)
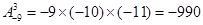
(Ⅱ)性质①、②均可推广,推广的形式分别是①
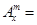
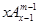 ,②
,②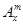
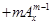
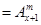 (
(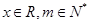 )
)证明:①当
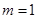 时,左边
时,左边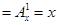 ,右边
,右边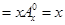 ,等式成立;
,等式成立;当
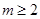 时,左边
时,左边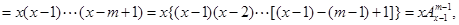
因此,
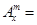
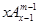 (
(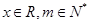 )成立.
)成立.②当
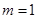 时,左边
时,左边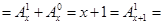 右边,等式成立;
右边,等式成立;当
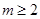 时,左边
时,左边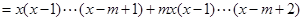
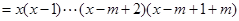

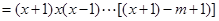
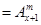 =右边
=右边因此,
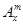
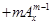
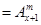 (
(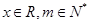 )成立.
)成立.(Ⅲ)
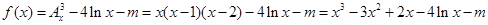
设函数
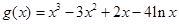 ,
,则函数
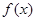 零点的个数等价于函数
零点的个数等价于函数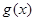 与
与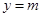 公共点的个数.
公共点的个数.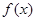 的定义域为
的定义域为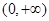
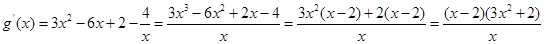
令
 ,得
,得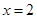
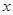 | 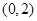 | 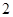 | 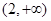 |
 | - | 0 | + |
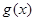 | 减 | 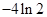 | 增 |
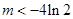 时,函数
时,函数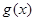 与
与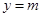 没有公共点,即函数
没有公共点,即函数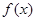 不存在零点,
不存在零点,当
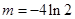 时,函数
时,函数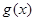 与
与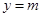 有一个公共点,即函数
有一个公共点,即函数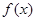 有且只有一个零点,
有且只有一个零点,当
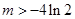 时,函数
时,函数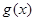 与
与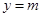 有两个公共点,即函数
有两个公共点,即函数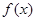 有且只有两个零点.
有且只有两个零点.点评:主要是考查了函数零点的求解以及组合数和排列数公式的运用,属于中档题。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
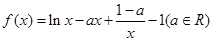
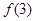 )处的切线方程
)处的切线方程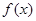 的单调递增区间
的单调递增区间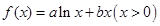 ,
,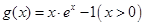 ,且函数
,且函数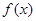 在点
在点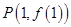 处的切线方程为
处的切线方程为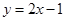 .
.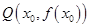 ,当
,当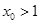 时,直线
时,直线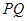 的斜率恒小于
的斜率恒小于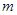 ,试求实数
,试求实数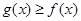 .
. ,
, ,
, (1)若
(1)若 ,求函数
,求函数 的极值;
的极值; 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围; 的图象上是否存在不同的两点
的图象上是否存在不同的两点 ,使线段
,使线段 的中点的横坐标
的中点的横坐标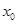 与直线
与直线 之间满足
之间满足 ?若存在,求出
?若存在,求出 与
与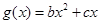 的图像都过点
的图像都过点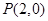 ,且它们在点
,且它们在点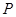 处有公共切线.
处有公共切线.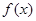 和
和 的表达式及在点
的表达式及在点 ,其中
,其中 ,求
,求 的单调区间.
的单调区间. 在
在 上可导,
上可导, ,则
,则 ______;
______;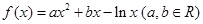
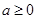 ,求
,求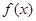 的单调区间;
的单调区间;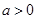 ,且对于任意
,且对于任意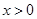 ,
,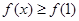 .试比较
.试比较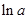 与
与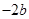 的大小.
的大小.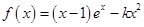 (其中
(其中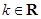 ).
).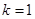 时,求函数
时,求函数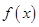 的单调区间;
的单调区间;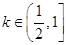 时,求函数
时,求函数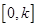 上的最大值
上的最大值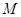 .
.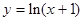
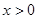 ,证明
,证明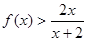 ;
;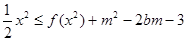 时
时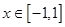 和
和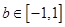 都恒成立,求实数
都恒成立,求实数 的取值范围。
的取值范围。