题目内容
一个只有有限项的等差数列,它的前5项和为34,最后5项的和为146,所有项的和为234,则它的第7项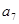 等于()
等于()
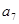 等于()
等于()| A. 22 | B. 21 | C. 19 | D. 18 |
D
解:设等差数列的项数为n,首项为a1,公差为d,
因为等差数列的前5项的和为34,最后5项的和为146,
所以a3=34 5 ,an-2=146
5 ,an-2=146 5 .
5 .
所以a1+an=36.
由等差数列的前n项和的公式可得:Sn=n(a1+an) 2 =18n=234,
2 =18n=234,
解得:n=13.
所以S13=13a7=234解得:a7=18.
故选D.
因为等差数列的前5项的和为34,最后5项的和为146,
所以a3=34
 5 ,an-2=146
5 ,an-2=146 5 .
5 .所以a1+an=36.
由等差数列的前n项和的公式可得:Sn=n(a1+an)
 2 =18n=234,
2 =18n=234,解得:n=13.
所以S13=13a7=234解得:a7=18.
故选D.

练习册系列答案
相关题目
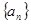 是首项
是首项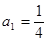 的等比数列,其前
的等比数列,其前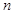 项和
项和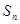 中
中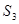 ,
,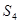 ,
,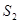 成
成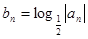 ,若
,若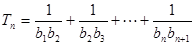 ,求证:
,求证: .
.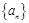 中,
中,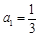 ,且前
,且前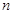 项的算术平均数等于第
项的算术平均数等于第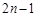 倍(
倍(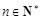 ). (即
). (即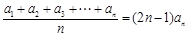
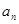 }的前
}的前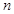 项和为
项和为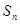 ,且
,且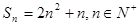 ,数列{
,数列{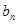 }满足
}满足 。
。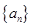 、{
、{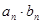 }的前
}的前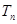 。
。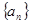 为等比数列,
为等比数列,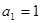 ,
,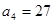 ,
,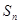 为等差数列
为等差数列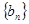 的前
的前 项和,
项和,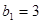 ,
,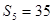 。
。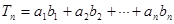 ,求
,求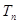 。
。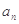 }的前n项和为
}的前n项和为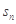 ,且S2=10,S5=55,则过点P(n,
,且S2=10,S5=55,则过点P(n,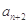 )(n∈N*)的直线的斜率为( )
)(n∈N*)的直线的斜率为( )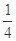
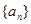 中,
中,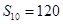 ,则
,则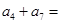 ( )
( ) 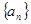 中,
中,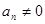 ,且满足
,且满足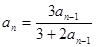
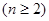 ,则数列
,则数列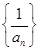 是( )
是( )